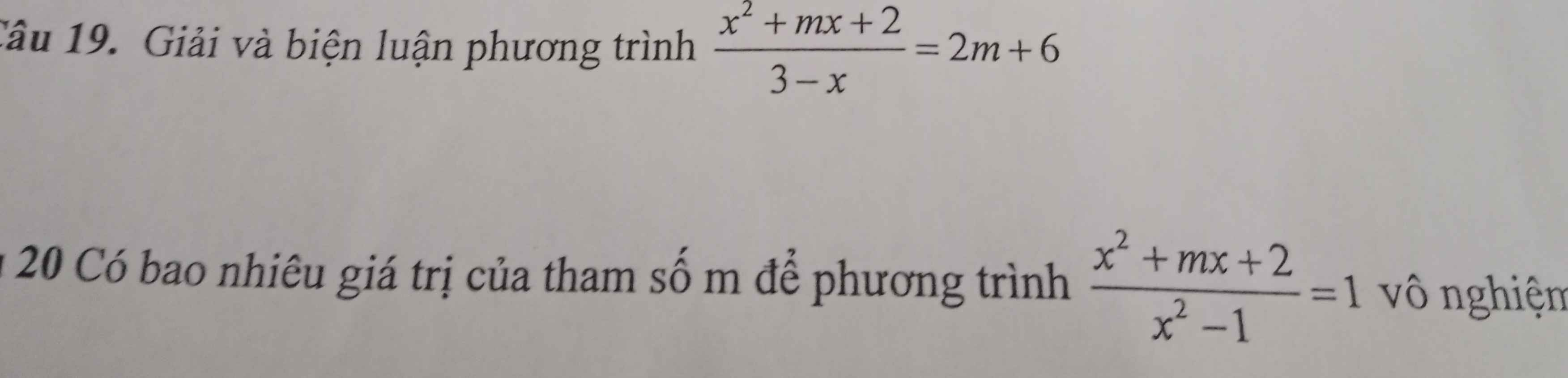Câu 19. Điều kiện: \(3-x\ne0\Leftrightarrow x\ne3\)
\(\dfrac{x^2+mx+2}{3-x}=2m+6\)
\(\Rightarrow x^2+mx+2=\left(2m+6\right)\left(3-x\right)\)
\(\Leftrightarrow x^2+mx+2=6m-2mx+18-6x\)
\(\Leftrightarrow x^2+3mx+6x-6m-16=0\)
\(\Leftrightarrow x^2+3\left(m+2\right)x-6m-16=0\) (*)
Coi phương trình (*) là phương trình bậc hai ẩn x, tham số m, ta có:
\(\Delta=\left[3\left(m+2\right)\right]^2+4\left(6m+16\right)\)
\(=9\left(m^2+4m+4\right)+24m+64\)
\(=9m^2+36m+36+24m+64\)
\(=9m^2+60m+100\)
Nhận thấy: \(\Delta=9m^2+60m+100=\left(3m+10\right)^2\ge0\) nên ta chỉ xét 2 trường hợp.
Trường hợp 1: \(m=-\dfrac{10}{3},\) khi đó phương trình có một nghiệm là: \(x=\dfrac{-3m-6}{2}\)
Trường hợp 2: \(m\ne-\dfrac{10}{3},\) khi đó phương trình có hai nghiệm phân biệt là: \(\left[{}\begin{matrix}x=2\\x=-3m-8\end{matrix}\right.\)
Câu 20. Điều kiện: \(x^2-1\ne0\Leftrightarrow\left\{{}\begin{matrix}x\ne1\\x\ne-1\end{matrix}\right.\)
\(\dfrac{x^2+mx+2}{x^2-1}=1\)
\(\Rightarrow x^2+mx+2=x^2-1\)
\(\Leftrightarrow mx+3=0\)
Điều kiện phương trình vô nghiệm là: \(m=0\)