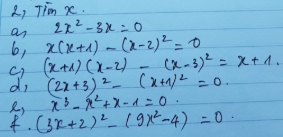\(P=\dfrac{\left(x+3\right)\left(x+2\right)+\left(x-3\right)\left(x-2\right)-2x^2-3x-6}{x^2-4}\)
\(=\dfrac{x^2+5x+6+x^2-5x+6-2x^2-3x-6}{x^2-4}=\dfrac{6-3x}{x^2-4}=\dfrac{-3\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{-3}{x+2}\)
\(b,\) \(P\left(3\right)=\dfrac{-3}{3+2}=\dfrac{-3}{5}\)
\(c,P=\dfrac{-3}{x+2}\in Z\Leftrightarrow x+2\inƯ\left(3\right)=\left\{\pm1;\pm3\right\}\Rightarrow x\in\left\{-3;-1;1;-5\right\}\left(tm\right)\)

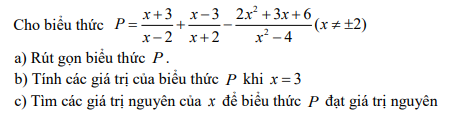










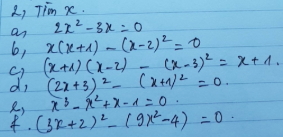 Không làm tắt
Không làm tắt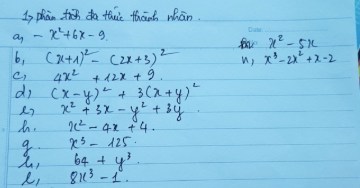 Ko làm tắt
Ko làm tắt