a) \(16x^2-8x+1-3\left(4x-1\right)=\left(4x-1\right)^2-3\left(4x-1\right)=\left(4x-1\right)\left(4x-1-3\right)=\left(4x-1\right)\left(4x-4\right)=4\left(4x-1\right)\left(x-1\right)\)
b) \(27x^3+8=\left(3x+2\right)\left(9x^2-6x+4\right)\)
c) \(-16x^4y^6-24x^5y^5-9x^6y^4=-x^4y^4\left(16y^2+24xy+9x^2\right)=-x^4y^4\left(4y+3x\right)^2\)
d) \(\left(ax+by\right)^2-\left(ay+bx\right)^2=\left(ax+by-ay-bx\right)\left(ax+by+ay+bx\right)=\left[a\left(x-y\right)-b\left(x-y\right)\right]\left[a\left(x+y\right)+b\left(x+y\right)\right]=\left(x-y\right)\left(x+y\right)\left(a-b\right)\left(a+b\right)\)
a)
\(=\left(4x-1\right)^2-3\left(4x-1\right)=\left(4x-1\right)\left(4x-1-3\right)=\left(4x-1\right)\left(4x-4\right)=4\left(x-1\right)\left(4x-1\right)\)
b)
\(=\left(3x+2\right)\left(9x^2-6x+4\right)\)
c)
\(=-x^4y^4\left(16y^2+24xy+9x^2\right)=-x^4y^4\left(4y+3x\right)^2\)
d)
\(=\left(ax+by-ay-bx\right)\left(ax+by+ay+bx\right)\)
\(=\left[a\left(x-y\right)+b\left(y-x\right)\right]\left[a\left(x+y\right)+b\left(x+y\right)\right]\)
\(=\left[a\left(x-y\right)-b\left(x-y\right)\right]\left(a+b\right)\left(x+y\right)\)
\(=\left(a-b\right)\left(a+b\right)\left(x-y\right)\left(x+y\right)=\left(a^2-b^2\right)\left(x^2-y^2\right)\)















 Không làm tắt
Không làm tắt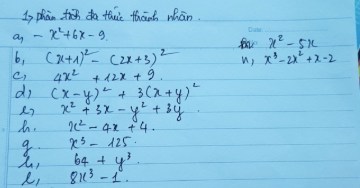 Ko làm tắt
Ko làm tắt