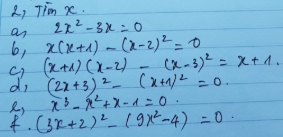\(1,=\left(x-y\right)\left(x+y\right)+\left(x+y\right)=\left(x-y+1\right)\left(x+y\right)\\ 2,=\left(2x-3y\right)\left(2x+3y\right)+2\left(2x-3y\right)=\left(2x-3y\right)\left(2x+3y+2\right)\\ 3,=\left(x+y\right)^2+\left(x+y\right)=\left(x+y\right)\left(x+y+1\right)\\ 4,=5\left(x-y\right)-\left(x-y\right)^2=\left(x-y\right)\left(5-x+y\right)\\ 5,=\left(x+1\right)^2-y^2=\left(x-y+1\right)\left(x+y+1\right)\\ 6,Giống.5\\ 7,=x^2-\left(y-1\right)^2=\left(x-y+1\right)\left(x+y-1\right)\\ 8,=\left(x+z\right)^2-\left(y-u\right)^2=\left(x+z-y+u\right)\left(x+z+y-u\right)\\ 9,=\left(x+y\right)^3+\left(x+y\right)=\left(x^2+2xy+y^2+1\right)\left(x+y\right)\\ 10,=x^3+y-3x^2y+3xy^2-x-y^3\\ =\left(x-y\right)^3-\left(x-y\right)=\left(x-y\right)\left(x^2-2xy+y^2-1\right)\)











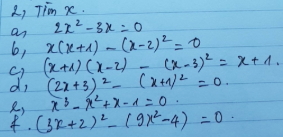 Không làm tắt
Không làm tắt Ko làm tắt
Ko làm tắt