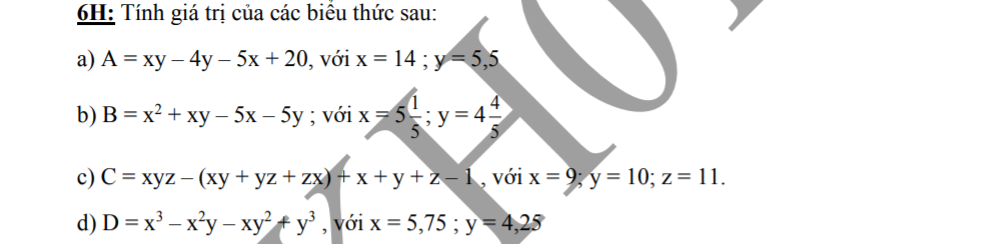a: Ta có: \(A=xy-4y-5x+20\)
\(=y\left(x-4\right)-5\left(x-4\right)\)
\(=\left(x-4\right)\left(y-5\right)\)
\(=10\cdot\dfrac{1}{2}=5\)
b: Ta có: \(B=x^2+xy-5x-5y\)
\(=x\left(x+y\right)-5\left(x+y\right)\)
\(=\left(x+y\right)\left(x-5\right)\)
\(=\left(\dfrac{26}{5}+\dfrac{24}{5}\right)\left(\dfrac{26}{5}-5\right)\)
\(=10\cdot\dfrac{1}{5}=2\)
a) \(A=xy-4y-5x+20=\left(x-4\right)\left(y-5\right)=\left(14-4\right)\left(5,5-5\right)=10.0,5=5\)
b)\(B=x^2+xy-5x-5y=\left(x+y\right)\left(x-5\right)=\left(5\dfrac{1}{5}+4\dfrac{4}{5}\right)\left(5\dfrac{1}{5}-5\right)=2\)
c) \(C=xyz-\left(xy+yz+xz\right)+x+y+z-1=\left(x-1\right)\left(y-1\right)\left(z-1\right)=\left(9-1\right)\left(10-1\right)\left(11-1\right)=720\)d) \(D=x^3-x^2y-xy^2+y^3=\left(x-y\right)^2\left(x+y\right)=\left(5,75-4,25\right)^2\left(5,75+4,25\right)=22,5\)