Trong kiểm soát không lưu, người ta dùng bộ ba số để xác định vị trí của máy bay. Người ta đã làm điều đó như thế nào?
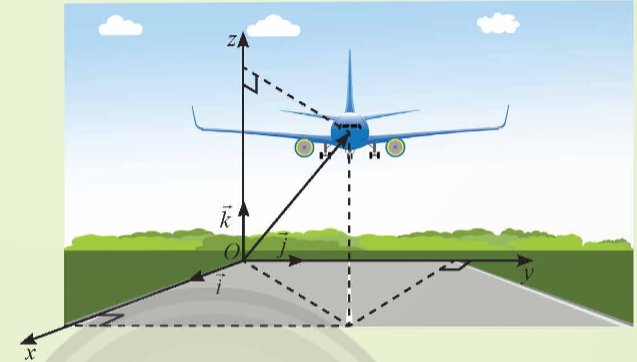
Trong kiểm soát không lưu, người ta dùng bộ ba số để xác định vị trí của máy bay. Người ta đã làm điều đó như thế nào?

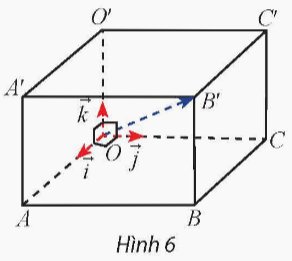
Cho hình lập phương OABC.O'A'B'C' có cạnh bằng 1. Đặt \(\overrightarrow{i}=\overrightarrow{OA};\overrightarrow{j}=\overrightarrow{OC};\overrightarrow{k}=\overrightarrow{OO'}\).
a) Nêu nhận xét về phương và độ dài của ba vectơ \(\overrightarrow{i},\overrightarrow{j},\overrightarrow{k}\).
b) Nêu nhận xét về ba trục tọa độ \(\left(O;\overrightarrow{i}\right);\left(O;\overrightarrow{j}\right),\left(O;\overrightarrow{k}\right)\).
Thảo luận (1)Hướng dẫn giảia) Độ dài 3 vecto \(\overrightarrow i \), \(\overrightarrow j \), \(\overrightarrow k \) bằng nhau: |\(\overrightarrow i \)| = |\(\overrightarrow j \)| = |\(\overrightarrow k \)|
b) Ba trục toạ độ \((O,\overrightarrow i )\) , \((O,\overrightarrow j )\) , \((O,\overrightarrow k )\) đôi một vuông góc với nhau
(Trả lời bởi Nguyễn Quốc Đạt)
Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 1, SA vuông góc với mặt phẳng đáy và có độ dài bằng 1 (Hình 4). Vẽ hệ trục tọa độ Oxyz có gốc O trùng với điểm A, các điểm B, D, S lần lượt nằm trên các tia Ox, Oy, Oz và chỉ ra các vectơ đơn vị trên các trục tọa độ.
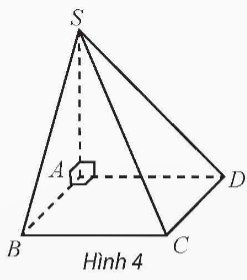
Thảo luận (1)Hướng dẫn giải
Các vecto đơn vị của Ox, Oy, Oz lần lượt là \(\overrightarrow i = \overrightarrow {AB} \), \(\overrightarrow j = \overrightarrow {AD} \), \(\overrightarrow k = \overrightarrow {AS} \)
(Trả lời bởi Nguyễn Quốc Đạt)
Một thiết kế cơ khí trong Hình 5a được biểu diễn trong không gian Oxyz như Hình 5b.
a) Hãy vẽ ba vectơ đơn vị \(\overrightarrow{i},\overrightarrow{j},\overrightarrow{k}\) lần lượt trên ba trục tọa độ Ox, Oy, Oz (mỗi vectơ đơn vị có độ dài bằng 1 m).
b) Biểu diễn các vectơ \(\overrightarrow{OC},\overrightarrow{OB},\overrightarrow{OA},\overrightarrow{AB}\) theo \(\overrightarrow{i},\overrightarrow{j},\overrightarrow{k}\).
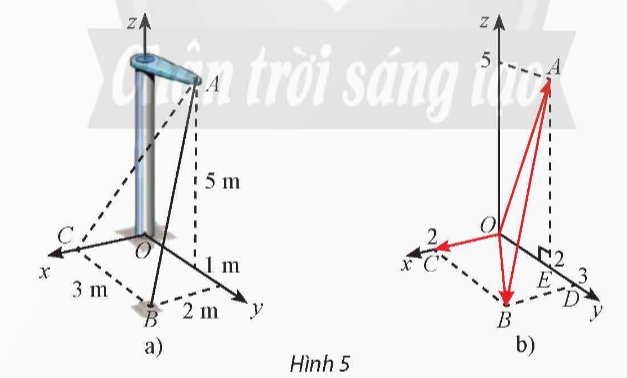
Thảo luận (1)Hướng dẫn giảia)
b) \(\overrightarrow {OC} = 2\overrightarrow i \)
\(\overrightarrow {OB} = 2\overrightarrow i + 3\overrightarrow j \)
\(\overrightarrow {OC} = 2\overrightarrow j + 3\overrightarrow k \)
(Trả lời bởi Nguyễn Quốc Đạt)
Cho hình hộp chữ nhật OABC.O'A'B'C' có cạnh OA = 3, OC = 5, OO' = 2. Vẽ ba vectơ đơn vị \(\overrightarrow{i},\overrightarrow{j},\overrightarrow{k}\) lần lượt trên các cạnh OA, OC, OO'. Biểu diễn \(\overrightarrow{OB'}\) theo ba vectơ \(\overrightarrow{i},\overrightarrow{j},\overrightarrow{k}\).
Thảo luận (1)Hướng dẫn giải\(\overrightarrow {OB'} = \overrightarrow {OO'} + \overrightarrow {OB} = \overrightarrow {OO'} + \overrightarrow {OA} + \overrightarrow {OC} = 2\overrightarrow k + 3\overrightarrow i + \overrightarrow {5j} \)
(Trả lời bởi Nguyễn Quốc Đạt)
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 5. Chọn hệ trục tọa độ Oxyz có gốc O trùng với A; các điểm B, D, A' lần lượt nằm trên các tia Ox, Oy, Oz. Xác định tọa độ các điểm B, C, C'.
Thảo luận (1)Hướng dẫn giải
Vi $\overrightarrow{O B}$ và $\vec{i}$ cùng hướng và $O B=5$ nên $\overrightarrow{O B}=5 \vec{i}$.
(Trả lời bởi Nguyễn Quốc Đạt)
Tương tự, ta có $\overrightarrow{O D}=5 \vec{j} ; \overrightarrow{O A^{\prime}}=5 \vec{k}$.
Theo quy tắc hình bình hành, ta có: $\overrightarrow{O C}=\overrightarrow{O B}+\overrightarrow{O D}=5 \vec{i}+5 \vec{j}$.
Theo quy tắc hình hộp, ta có: $\overrightarrow{O C^{\prime}}=\overrightarrow{O B}+\overrightarrow{O D}+\overrightarrow{O A^{\prime}}=5 \vec{i}+5 \vec{j}+5 \vec{k}$.
Do đó $B(5 ; 0 ; 0), C(5 ; 5 ; 0), C^{\prime}(5 ; 5 ; 5)$.
Trong không gian Oxyz, cho vectơ \(\overrightarrow{a}\). Vẽ điểm A sao cho \(\overrightarrow{OA}=\overrightarrow{a}\). Gọi (a1; a2; a3) là tọa độ của điểm A. Hãy biểu diễn \(\overrightarrow{a}\) theo ba vectơ đơn vị \(\overrightarrow{i},\overrightarrow{j},\overrightarrow{k}\).
Thảo luận (1)Hướng dẫn giảiTa có: \(\overrightarrow a \)= \({a_1}\overrightarrow i \)+\({a_2}\overrightarrow j \)+\({a_3}\overrightarrow k \)
(Trả lời bởi Nguyễn Quốc Đạt)
Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 2, SA vuông góc với mặt phẳng đáy và có độ dài bằng 3 (Hình 11).
a) Vẽ hệ trục tọa độ Oxyz có gốc O trùng với điểm A, các điểm B, D, S lần lượt nằm trên các tia Ox, Oy, Oz và chỉ ra các vectơ đơn vị trên các trục tọa độ.
b) Trong hệ tọa độ nói trên, tìm tọa độ các vectơ \(\overrightarrow{AB},\overrightarrow{AD},\overrightarrow{AS}\) và \(\overrightarrow{AM}\) với M là trung điểm của cạnh SC.
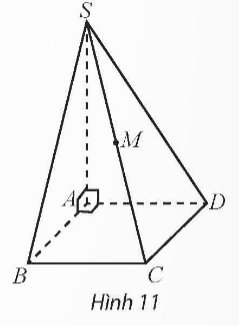
Thảo luận (1)Hướng dẫn giảia)
Các vecto đơn vị của Ox, Oy, Oz lần lượt là \(\overrightarrow i \), \(\overrightarrow j \), \(\overrightarrow k \)
b) \(\overrightarrow {AB} = 2\overrightarrow i = > \overrightarrow {AB} = (2;0;0)\)
\(\overrightarrow {AD} = 2\overrightarrow j = > \overrightarrow {AD} = (0;2;0)\)
\(\overrightarrow {AS} = 3\overrightarrow k = > \overrightarrow {AS} (0;0;3)\)
\(\overrightarrow {AM} = \frac{1}{2}(\overrightarrow {AS} + \overrightarrow {AC} ) = \frac{1}{2}(3\overrightarrow k + 2\overrightarrow i + 2\overrightarrow j ) = \overrightarrow i + \overrightarrow j + \frac{3}{2}\overrightarrow k = > \overrightarrow {AM} = (1;1;\frac{3}{2})\)
(Trả lời bởi Nguyễn Quốc Đạt)
Một máy bay đang cất cánh từ phi trường. Với hệ tọa độ Oxyz được thiết lập như Hình 12, cho biết M là vị trí của máy bay, OM = 14, \(\widehat{NOB}=32^o,\widehat{MOC}=65^o\). Tìm tọa độ điểm M.
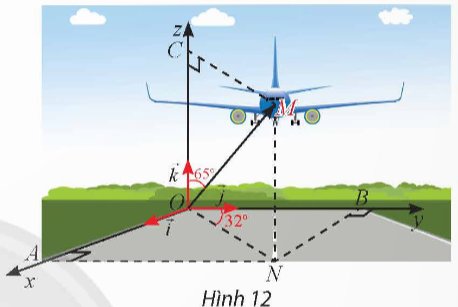
Thảo luận (1)Hướng dẫn giảiXét tam giác COM vuông tại C:
\(CO = OM.\cos 65^\circ = 14.\cos 65^\circ \approx 5,92\)
\(CM = OM.\sin 65^\circ = 14.\sin 65^\circ \approx 12,69\)
Xét tam giác BON vuông tại B:
\(OB = ON.\cos 32^\circ = CM.\cos 32^\circ = 12,69.\cos 32^\circ \approx 10,76\)
Xét tam giác AON vuông tại A:
\(OA = ON.\cos (90^\circ - 32^\circ ) = 12,69.\cos 58^\circ = 6,72\)
Vậy tọa độ của M là (6,72; 10,76; 5,92)
(Trả lời bởi Nguyễn Quốc Đạt)
Trong không gian Oxyz, biết
a) $\vec{a}=5 \vec{i}+7 \vec{j}-3 \vec{k}, \vec{b}=2 \vec{i}+4 \vec{k}$. Tìm tọa độ các vectơ $\mathrm{a}, \mathrm{b}$.
b) $\overrightarrow{O M}=4 \vec{i}-\vec{j}+3 \vec{k}, \overrightarrow{O N}=8 \vec{i}-5 \vec{j}$. Tìm tọa độ điểm $\mathrm{M}, \mathrm{N}$.
Thảo luận (1)Hướng dẫn giảia) \(\overrightarrow a = 5\overrightarrow i + 7\overrightarrow j - 3\overrightarrow k = (5;7; - 3)\)
\(\overrightarrow b = 2\overrightarrow i + 4\overrightarrow k = (2;0;4)\)
b) \(\overrightarrow {OM} = 4\overrightarrow i - \overrightarrow j + 3\overrightarrow k = (4; - 1;3)\) => M(4;-1;3)
\(\overrightarrow {ON} = 8\overrightarrow i - 5\overrightarrow j = (8;-5;0)\) => N(8;-5;0)
(Trả lời bởi Nguyễn Quốc Đạt)