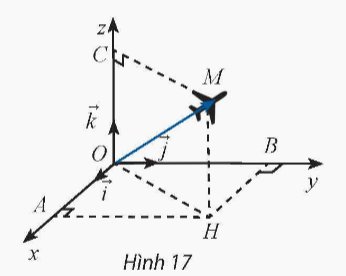
Trong không gian Oxyz, biết:
a) \(\overrightarrow{a}=\left(-2;5;-7\right),\overrightarrow{b}=\left(4;0;1\right)\). Tính \(\overrightarrow{a},\overrightarrow{b}\) theo các vectơ \(\overrightarrow{i},\overrightarrow{j},\overrightarrow{k}\).
b) A(7; -2; 1), B(0; 5; 0). Tính \(\overrightarrow{OA},\overrightarrow{OB}\) theo các vectơ \(\overrightarrow{i},\overrightarrow{j},\overrightarrow{k}\).