Trong không gian, làm thế nào để biểu diễn độ dịch chuyển tín hiệu vô tuyến từ máy bay đến trạm kiểm soát trên mặt đất?
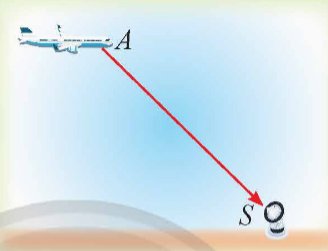
Trong không gian, làm thế nào để biểu diễn độ dịch chuyển tín hiệu vô tuyến từ máy bay đến trạm kiểm soát trên mặt đất?

Nhắc lại định nghĩa vectơ trong mặt phẳng.
Có thể định nghĩa vectơ trong không gian như đã định nghĩa vectơ trong mặt phẳng không?
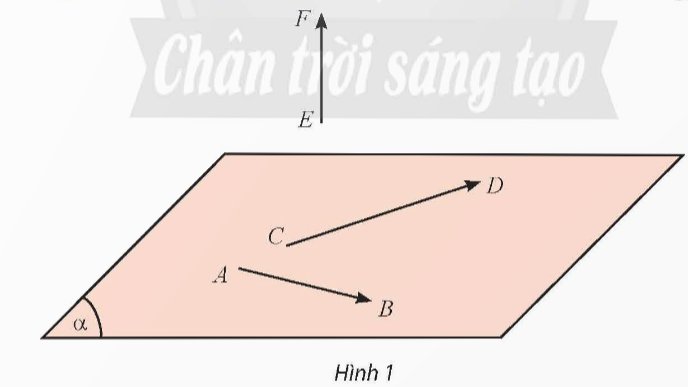
Thảo luận (1)Hướng dẫn giải- Vecto trong mặt phẳng tọa độ là một đoạn thẳng có hướng, có điểm đầu và cuối, nằm trong hệ trục tọa độ Oxy với tọa độ là , trong đó là hoành độ và là tung độ
- Vecto trong không gian có thể được định nghĩa tương tự như vecto trong mặt phẳng
(Trả lời bởi Nguyễn Quốc Đạt)
Trong hoạt động khởi động, tìm vectơ biểu diễn độ dịch chuyển tín hiệu vô tuyến từ vị trí A của máy bay đến vị trí S của trạm kiểm soát.
Thảo luận (1)Hướng dẫn giảiVectơ biểu diễn độ dịch chuyển tín hiệu vô tuyến từ vị trí A của máy bay đến vị trí S của trạm kiểm soát là \(\overrightarrow {AS} \)
(Trả lời bởi Nguyễn Quốc Đạt)
Cho hình chóp tứ giác đều S.ABCD.
a) Chỉ ra các vectơ có điểm đầu là S và điểm cuối là các đỉnh của đa giác đáy.
b) Tìm các vectơ có độ dài bằng độ dài của vectơ \(\overrightarrow{SA}\).
c) Tìm các vectơ đối của vectơ \(\overrightarrow{CB}\).
Thảo luận (1)Hướng dẫn giải
a) Các vecto: \(\overrightarrow {SA} ;\overrightarrow {SB} \overrightarrow {;SC} \overrightarrow {;SD} \)
b) Các vectơ có độ dài bằng độ dài của vectơ \(\overrightarrow {SA} \): \(\overrightarrow {SB} \overrightarrow {;SC} \overrightarrow {;SD} \)
c) Các vectơ đối của vectơ \(\overrightarrow {CB} \): \(\overrightarrow {AD} \)
(Trả lời bởi Nguyễn Quốc Đạt)
Trong Hình 4, cho biết ba vectơ \(\overrightarrow{F_1},\overrightarrow{F_2},\overrightarrow{F_3}\) biểu diễn lực căng của các sợi dây cáp AB, AC, AD tác dụng lên vật nặng. Giá của ba vectơ này có cùng nằm trên một mặt phẳng không?
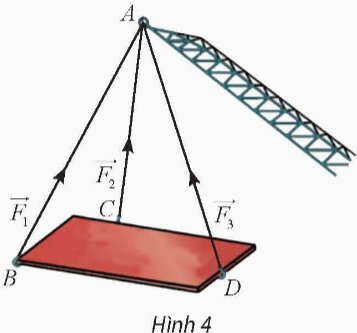
Thảo luận (1)Hướng dẫn giảiGiá của 3 vecto \(\overrightarrow {{F_1}} ;\overrightarrow {{F_2}} ;\overrightarrow {{F_3}} \) không cùng nằm trên một mặt phẳng
(Trả lời bởi Nguyễn Quốc Đạt)
Cho hình hộp ABCD.A'B'C'D' (Hình 5).
a) Trong mặt phẳng (ABCD), tìm vectơ tổng \(\overrightarrow{AB}+\overrightarrow{BC}\). Trong mặt phẳng (A'B'C'D'), tìm vectơ tổng \(\overrightarrow{A'B}'+\overrightarrow{B'C'}\)
b) Tìm mối liên hệ giữa các cặp vectơ \(\overrightarrow{AB}\) và \(\overrightarrow{A'B'}\), \(\overrightarrow{BC}\) và \(\overrightarrow{B'C'}\), \(\overrightarrow{AC}\) và \(\overrightarrow{A'C'}\).
c) Giải thích tại sao \(\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{A'B'}+\overrightarrow{B'C'}\).
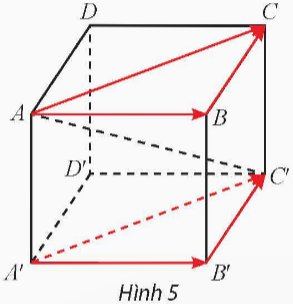
Thảo luận (1)Hướng dẫn giảia) \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
b) \(\overrightarrow {BD'} = \overrightarrow {B'D'} \)
c) \(\overrightarrow {AB} + \overrightarrow {B'D'} = \overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {AD} \)
(Trả lời bởi Nguyễn Quốc Đạt)
Cho hình hộp ABCD.A'B'C'D'.
a) Tìm các vectơ tổng \(\overrightarrow{AB}+\overrightarrow{AD},\overrightarrow{AC}+\overrightarrow{AA'}\).
b) Dùng kết quả của câu a và tính chất kết hợp của phép cộng vectơ để chứng minh \(\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AA'}=\overrightarrow{AC'}\).
Thảo luận (1)Hướng dẫn giải
a) \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \);\(\overrightarrow {AC} + \overrightarrow {AA'} = \overrightarrow {AC'} \)
b) \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC} + \overrightarrow {AA'} = \overrightarrow {AC'} \)
(Trả lời bởi Nguyễn Quốc Đạt)
Cho hình hộp ABCD.EFGH. Tìm các vectơ:
a) \(\overrightarrow{DA}+\overrightarrow{DC}+\overrightarrow{DH}\). b) \(\overrightarrow{HE}+\overrightarrow{GC}+\overrightarrow{AB}\).
Thảo luận (1)Hướng dẫn giải
a) \(\overrightarrow {DA} + \overrightarrow {DC} + \overrightarrow {DH} = \overrightarrow {DB} + \overrightarrow {DH} = \overrightarrow {DF} \)
b) \(\overrightarrow {HE} + \overrightarrow {GC} + \overrightarrow {AB} = \overrightarrow {HE} + \overrightarrow {HD} + \overrightarrow {HG} = \overrightarrow {HB} \)
(Trả lời bởi Nguyễn Quốc Đạt)
Cho hình hộp ABCD.A'B'C'D'
a) Trong mặt phẳng (ABCD), tìm vectơ hiệu \(\overrightarrow{AB}-\overrightarrow{AD}\). Trong mặt phẳng (ABCD), tìm vectơ hiệu \(\overrightarrow{A'B'}-\overrightarrow{A'D'}\).
b) Tìm mối liên hệ giữa các cặp vectơ \(\overrightarrow{AB}\) và \(\overrightarrow{A'B'}\), \(\overrightarrow{AD}\) và \(\overrightarrow{A'D'}\), \(\overrightarrow{DB}\) và \(\overrightarrow{D'B'}\).
c) Giải thích tại sao \(\overrightarrow{AB}-\overrightarrow{AD}=\overrightarrow{A'B'}-\overrightarrow{A'D'}\).
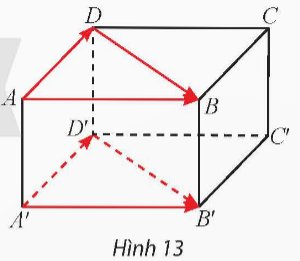
Thảo luận (1)Hướng dẫn giảia) $\overrightarrow{A B}-\overrightarrow{A D}=\overrightarrow{D B} ; \overrightarrow{A^{\prime} B^{\prime}}-\overrightarrow{A^{\prime} D^{\prime}}=\overrightarrow{D^{\prime} B^{\prime}}$
b) Vi $A A^{\prime} B^{\prime} B$ là hình bình hành, suy ra $A B / / A^{\prime} B^{\prime}$ và $A B=A^{\prime} B^{\prime}$.Ta có hai vectơ $\overrightarrow{A B}$ và $\overrightarrow{A^{\prime} B^{\prime}}$ cùng hướng và có độ dài bằng nhau nên $\overrightarrow{A B}=\overrightarrow{A^{\prime} B^{\prime}}$
Tương tự $\overrightarrow{A D}=\overrightarrow{A^{\prime} D^{\prime}} ; \overrightarrow{D B}=\overrightarrow{D^{\prime} B^{\prime}}$.
(Trả lời bởi Nguyễn Quốc Đạt)
c) vi $\overrightarrow{A B}-\overrightarrow{A D}=\overrightarrow{D B} ; \overrightarrow{A^{\prime} B^{\prime}}-\overrightarrow{A^{\prime} D^{\prime}}=\overrightarrow{D^{\prime} B^{\prime}}$ mà $\overrightarrow{D B}=\overrightarrow{D^{\prime} B^{\prime}}$ nên $\overrightarrow{A B}-\overrightarrow{A D}=\overrightarrow{A^{\prime} B^{\prime}}-\overrightarrow{A^{\prime} D^{\prime}}$
Cho tứ diện ABCD có M và N lần lượt là trung điểm của AB và CD. Tìm các vectơ:
a) \(\overrightarrow{BM}+\overrightarrow{AC}+\overrightarrow{ND}\). b) \(\overrightarrow{AD}-\overrightarrow{AM}+\overrightarrow{NC}\).
Thảo luận (1)Hướng dẫn giải
a) $\overrightarrow{B M}+\overrightarrow{A C}+\overrightarrow{N D}=\overrightarrow{B M}+\overrightarrow{A M}+\overrightarrow{M C}+\overrightarrow{N D}=\overrightarrow{M N}+\overrightarrow{N C}+\overrightarrow{N D}=\overrightarrow{M N}$
(Trả lời bởi Nguyễn Quốc Đạt)
(Do $M$ và $N$ lần lượt là trung điểm của $A B$ và $C D$ nên $\overrightarrow{N C}+\overrightarrow{N D}=\overrightarrow{0} ; \overrightarrow{B M}+\overrightarrow{A M}=\overrightarrow{0})$.
b) $\overrightarrow{A D}-\overrightarrow{A M}+\overrightarrow{N C}=\overrightarrow{M D}+\overrightarrow{N C}=\overrightarrow{M N}+\overrightarrow{N D}+\overrightarrow{N C}=\overrightarrow{M N}$ (vì $\overrightarrow{N D}+\overrightarrow{N C}=\overrightarrow{0}$ ).