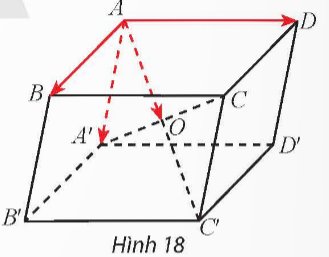
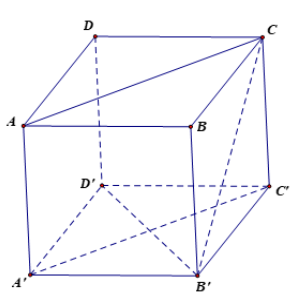
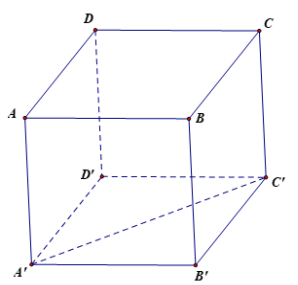
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng đơn vị. Tìm độ dài các vectơ sau đây:
a) \(\overrightarrow{a}=\overrightarrow{BA}+\overrightarrow{BC}+\overrightarrow{BB'}\); b) \(\overrightarrow{b}=\overrightarrow{BC}-\overrightarrow{BA}-\overrightarrow{C'A}\).