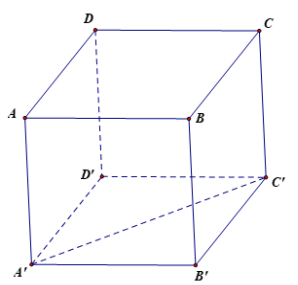
a) Vì ABB'A' là hình vuông nên $\overrightarrow{A B}=\overrightarrow{A^{\prime} B^{\prime}}$.
Do đó $\left(\overrightarrow{A B}, \overrightarrow{A^{\prime} C^{\prime}}\right)=\left(\overrightarrow{A^{\prime} B^{\prime}}, \overrightarrow{A^{\prime} C^{\prime}}\right)=\widehat{B^{\prime} A^{\prime} C^{\prime}}=45^{\circ}$ (do $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ là hình vuông nên $A^{\prime} C^{\prime}$ là phân giác của góc $\left.\widehat{D^{\prime} A^{\prime} B^{\prime}}\right)$.
Vì $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ là hình vuông cạnh bằng 1 nên $A^{\prime} C^{\prime}=\sqrt{2}$.
Ta có $\overrightarrow{A B} \cdot \overrightarrow{A^{\prime} C^{\prime}}=|\overrightarrow{A B}| \cdot\left|\overrightarrow{A^{\prime} C^{\prime}}\right| \cdot \cos \left(\overrightarrow{A B}, \overrightarrow{A^{\prime} C^{\prime}}\right)=1 \cdot \sqrt{2} \cdot \cos 45^{\circ}=1$.
Vi ACC'A' là hình bình hành nên $\overrightarrow{C C^{\prime}}=\overrightarrow{A A^{\prime}}$.
Do đó $\left(\overrightarrow{A B}, \overrightarrow{C C^{\prime}}\right)=\left(\overrightarrow{A B}, \overrightarrow{A A^{\prime}}\right)=\widehat{B A A^{\prime}}=90^{\circ}$.
Do đó $\overrightarrow{A B} \perp \overrightarrow{C C^{\prime}}$. Suy ra $\overrightarrow{A B} \cdot \overrightarrow{C C^{\prime}}=0$.
b) $\left(\overrightarrow{A C}, \overrightarrow{A C^{\prime}}\right)=\widehat{C A C^{\prime}}$.
Ta có $A C^{\prime}$ là đường chéo của hình lập phương cạnh bằng 1 nên $A C^{\prime}=\sqrt{3}$.
AC là đường chéo của hình vuông ABCD cạnh bằng 1 nên $A C=\sqrt{2}$.
Xét DACC' có $\cos \widehat{C A C^{\prime}}=\frac{A C^2+A C^2-C C^{\prime 2}}{2 \cdot A C \cdot A C^{\prime}}=\frac{2+3-1}{2 \cdot \sqrt{2} \cdot \sqrt{3}}=\frac{\sqrt{6}}{3} \Rightarrow \widehat{C A C^{\prime}} \approx 35^{\circ} 16^{\prime}$
$\operatorname{Vậy}\left(\overrightarrow{A C}, \overrightarrow{A C^{\prime}}\right) \approx 35^{\circ} 16^{\prime}$.


