Question

Cho tứ diện ABCD có M và N lần lượt là trung điểm của AB và CD. Tìm các vectơ:

a) \(\overrightarrow{BM}+\overrightarrow{AC}+\overrightarrow{ND}\).                     b) \(\overrightarrow{AD}-\overrightarrow{AM}+\overrightarrow{NC}\).

Answer 1

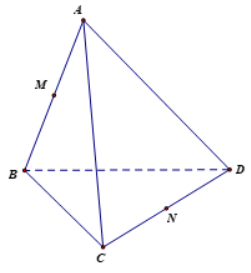
a) $\overrightarrow{B M}+\overrightarrow{A C}+\overrightarrow{N D}=\overrightarrow{B M}+\overrightarrow{A M}+\overrightarrow{M C}+\overrightarrow{N D}=\overrightarrow{M N}+\overrightarrow{N C}+\overrightarrow{N D}=\overrightarrow{M N}$
(Do $M$ và $N$ lần lượt là trung điểm của $A B$ và $C D$ nên $\overrightarrow{N C}+\overrightarrow{N D}=\overrightarrow{0} ; \overrightarrow{B M}+\overrightarrow{A M}=\overrightarrow{0})$.
b) $\overrightarrow{A D}-\overrightarrow{A M}+\overrightarrow{N C}=\overrightarrow{M D}+\overrightarrow{N C}=\overrightarrow{M N}+\overrightarrow{N D}+\overrightarrow{N C}=\overrightarrow{M N}$ (vì $\overrightarrow{N D}+\overrightarrow{N C}=\overrightarrow{0}$ ).