Trong không gian Oxyz, làm thế nào để xác định một mặt phẳng bằng phương pháp tọa độ?
Trong không gian Oxyz, làm thế nào để xác định một mặt phẳng bằng phương pháp tọa độ?

a) Cho vectơ \(\overrightarrow{n}\) khác \(\overrightarrow{0}\). Qua một điểm M0 cố định trong không gian, có bao nhiêu mặt phẳng (α) vuông góc với giá của vectơ \(\overrightarrow{n}\)?
b) Cho hai vectơ \(\overrightarrow{a},\overrightarrow{b}\) không cùng phương. Qua một điểm M0 cố định trong không gian, có bao nhiêu mặt phẳng (α) song song hoặc chứa giá của hai vectơ \(\overrightarrow{a},\overrightarrow{b}\)?
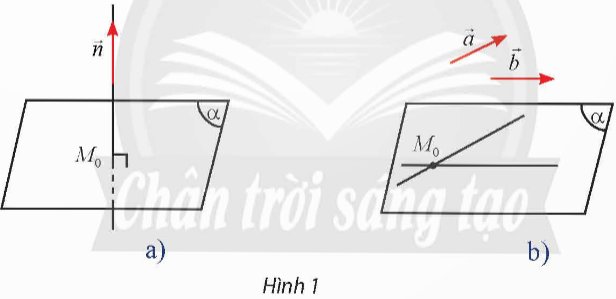
Thảo luận (1)Hướng dẫn giảia) Với một điểm và một đường thẳng trong không gian, có duy nhất một mặt phẳng đi qua điểm và vuông góc với đường thẳng đó. Vậy có duy nhất một mặt phẳng \(\left( \alpha \right)\) đi qua điểm \({M_0}\) và vuông góc với giá của vectơ \(\vec n\).
b) Do hai vectơ \(\vec a\) và \(\vec b\) không cùng phương, giá của hai vectơ (lần lượt là \(a\) và \(b\)) không song song hay trùng nhau. Chọn đường thẳng \(a'\) sao cho \(a'\) song song hoặc trùng với \(a\) và \(a'\) cắt \(b\). Khi đó, có duy nhất một mặt phẳng \(\left( \beta \right)\) chứa \(a'\) và \(b\).
Nếu \({M_0} \in \left( \beta \right)\) thì mặt phẳng \(\left( \beta \right)\) là mặt phẳng duy nhất đi qua \({M_0}\) và song song hoặc chứa giá của hai vectơ \(\vec a\) và \(\vec b\).
Nếu \({M_0} \notin \left( \beta \right)\), thì trong không gian, tồn tại duy nhất mặt phẳng \(\left( \alpha \right)\) đi qua \({M_0}\) và song song với \(\left( \beta \right)\). Khi đó, \(\left( \alpha \right)\) song song hoặc chứa giá của hai vectơ \(\vec a\) và \(\vec b\).
(Trả lời bởi datcoder)
Trong không gian Oxyz, cho ba điểm A(3; 0; 0), B(0; 4; 0), C(0; 0; 5).
a) Tìm tọa độ của một cặp vectơ chỉ phương của mặt phẳng (ABC).
b) Tìm tọa độ của một vectơ pháp tuyến của mặt phẳng (OAB).
Thảo luận (1)Hướng dẫn giảia) Ta có \(\overrightarrow {AB} \left( { - 3;4;0} \right)\) và \(\overrightarrow {AC} \left( { - 3;0;5} \right)\) là hai vectơ không cùng phương và có giá nằm trong mặt phẳng \(\left( {ABC} \right)\). Vậy \(\overrightarrow {AB} \left( { - 3;4;0} \right)\) và \(\overrightarrow {AC} \left( { - 3;0;5} \right)\) là một cặp vectơ chỉ phương của mặt phẳng \(\left( {ABC} \right)\).
b) Ta thấy rằng \(A\left( {3;0;0} \right) \in Ox\), \(B\left( {0;4;0} \right) \in Oy\), \(C\left( {0;0;5} \right) \in Oz\).
Dễ dàng suy ra rằng \(OC \bot OA\) và \(OC \bot OB\), từ đó \(OC \bot \left( {OAB} \right)\).
Hơn nữa, vectơ \(\overrightarrow {OC} \left( {0;0;5} \right)\) có giá là đường thẳng \(OC\). Do đó \(\overrightarrow {OC} \left( {0;0;5} \right)\) là một vectơ pháp tuyến của mặt phẳng \(\left( {OAB} \right)\).
(Trả lời bởi datcoder)
Một lăng kính có dạng hình lăng trụ đứng có đáy là tam giác đều ở Hình 3a được vẽ lại như Hình 3b. Tìm một cặp vectơ chỉ phương và một vectơ pháp tuyến của mặt phẳng (A'B'C').
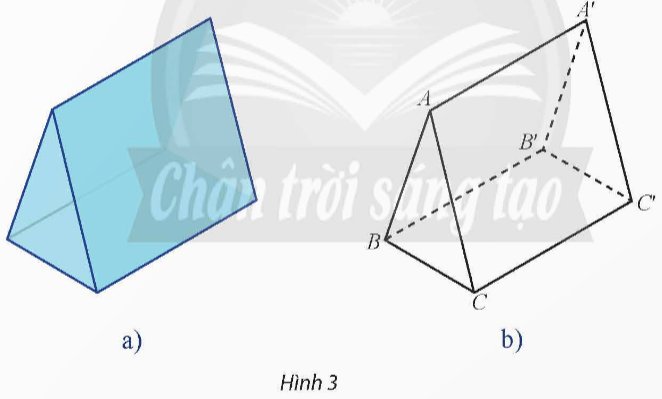
Thảo luận (1)Hướng dẫn giảiTa thấy rằng \(\overrightarrow {A'B'} \) và \(\overrightarrow {A'C'} \) là hai vectơ không cùng phương và có giá nằm trong mặt phẳng \(\left( {A'B'C'} \right)\). Suy ra \(\overrightarrow {A'B'} \) và \(\overrightarrow {A'C'} \) là một cặp vectơ chỉ phương của mặt phẳng \(\left( {A'B'C'} \right)\).
Do \(ABC.A'B'C'\) là lăng trụ đứng, nên ta có \(BB' \bot \left( {A'B'C'} \right)\).
Mặt khác, vectơ \(\overrightarrow {BB'} \) có giá là đường thẳng \(BB'\), do đó \(\overrightarrow {BB'} \) là một vectơ pháp tuyến của mặt phẳng \(\left( {A'B'C'} \right)\).
(Trả lời bởi datcoder)
Trong không gian Oxyz, cho mặt phẳng (α) có cặp vectơ chỉ phương \(\overrightarrow{a}=\left(a_1,a_2,a_3\right),\overrightarrow{b}=\left(b_1,b_2,b_3\right)\). Xét vectơ \(\overrightarrow{n}=\left(a_2b_3-a_3b_2;a_3b_1-a_1b_3;a_1b_2-a_2b_1\right)\).
a) Vectơ \(\overrightarrow{n}\) có khác \(\overrightarrow{0}\) hay không?
b) Tính \(\overrightarrow{a}.\overrightarrow{n};\overrightarrow{b}.\overrightarrow{n}\).
c) Vectơ \(\overrightarrow{n}\) có phải là vectơ pháp tuyến của mặt phẳng (α) không?
Thảo luận (1)Hướng dẫn giảia) Giả sử \(\vec n = \vec 0\), khi đó \({a_2}{b_3} - {a_3}{b_2} = {a_3}{b_1} - {a_1}{b_3} = {a_1}{b_2} - {a_2}{b_1} = 0\).
Với trường hợp \({b_1}\), \({b_2}\), \({b_3}\) cùng khác 0, ta suy ra \(\frac{{{a_1}}}{{{b_1}}} = \frac{{{a_2}}}{{{b_2}}} = \frac{{{a_3}}}{{{b_3}}}\), điều này có nghĩa \(\vec a\) và \(\vec b\) là hai vectơ cùng phương.
Nếu \({b_1} = 0\) thì \({a_1} = 0\), ta vẫn thu được kết quả \(\vec a\) và \(\vec b\) là hai vectơ cùng phương.
Các trường hợp còn lại cho ra kết quả tương tự.
Như vậy \(\vec a\) và \(\vec b\) là hai vectơ cùng phương.
Mặt khác, do \(\vec a\) và \(\vec b\) là một cặp vectơ chỉ phương của \(\left( \alpha \right)\), nên \(\vec a\) và \(\vec b\) là hai vectơ không cùng phương, mâu thuẫn.
Như vậy \(\vec n \ne \vec 0\).
b) Ta có:
+)\(\vec a.\vec n = {a_1}\left( {{a_2}{b_3} - {a_3}{b_2}} \right) + {a_2}\left( {{a_3}{b_1} - {a_1}{b_3}} \right) + {a_3}\left( {{a_1}{b_2} - {a_2}{b_1}} \right)\)
\( = {a_1}{a_2}{b_3} - {a_1}{a_3}{b_2} + {a_2}{a_3}{b_1} - {a_2}{a_1}{b_3} + {a_3}{a_1}{b_2} - {a_3}{a_2}{b_1} = 0\)
+) \(\vec b.\vec n = {b_1}\left( {{a_2}{b_3} - {a_3}{b_2}} \right) + {b_2}\left( {{a_3}{b_1} - {a_1}{b_3}} \right) + {b_3}\left( {{a_1}{b_2} - {a_2}{b_1}} \right)\)
\( = {b_1}{a_2}{b_3} - {b_1}{a_3}{b_2} + {b_2}{a_3}{b_1} - {b_2}{a_1}{b_3} + {b_3}{a_1}{b_2} - {b_3}{a_2}{b_1} = 0\)
Như vậy \(\vec a.\vec n = \vec b.\vec n = 0\).
c) Theo câu b, ta có \(\vec a.\vec n = \vec b.\vec n = 0\), điều này có nghĩa là \(\vec n\) có giá vuông góc với giá của \(\vec a\) và \(\vec b\). Mà \(\vec a\) và \(\vec b\) là một cặp vectơ chỉ phương của \(\left( \alpha \right)\), nên \(\vec n\) có giá vuông góc với mặt phẳng \(\left( \alpha \right)\). Như vậy \(\vec n\) là một vectơ pháp tuyến của \(\left( \alpha \right)\).
(Trả lời bởi datcoder)
Cho mặt phẳng (Q) đi qua ba điểm A(1; 1; 1), B(−1; 1; 5), C(10; 7; −1). Tìm cặp vectơ chỉ phương và một vectơ pháp tuyến của (Q).
Thảo luận (1)Hướng dẫn giảiTa có \(\left( Q \right)\) đi qua \(A\left( {1;1;1} \right)\), \(B\left( { - 1;1;5} \right)\), \(C\left( {10;7; - 1} \right)\), nên nó sẽ có một cặp vectơ chỉ phương là \(\overrightarrow {AB} \left( { - 2;0;4} \right)\) và \(\overrightarrow {AC} \left( {9;6; - 2} \right)\).
Tích có hướng của hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) là:
\(\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( {0.\left( { - 2} \right) - 4.6;4.9 - \left( { - 2} \right).\left( { - 2} \right); - 2.6 - 0.9} \right) = \left( { - 24;32; - 12} \right)\)
Do đó, mặt phẳng \(\left( Q \right)\) nhận \(\vec n = \frac{1}{4}\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( { - 6;8; - 3} \right)\) làm một vectơ pháp tuyến.
(Trả lời bởi datcoder)
Cho biết hai vectơ \(\overrightarrow{a}=\left(2;1;1\right),\overrightarrow{b}=\left(1;-2;0\right)\) có giá lần lượt song song với ngón trỏ và ngón giữa của bàn tay trong Hình 5. Tìm vectơ \(\overrightarrow{n}\) có giá song song với ngón cái. (Xem như ba ngón tay nói trên tạo thành ba đường thẳng đôi một vuông góc).
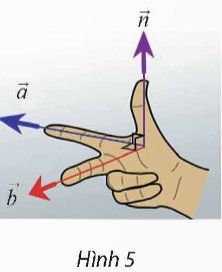
Thảo luận (1)Hướng dẫn giảiTheo hình vẽ, do vectơ \(\vec n\) có giá vuông góc lần lượt với giá của hai vectơ \(\vec a\) và \(\vec b\), nên có thể chọn vectơ \(\vec n\) là tích có hướng của hai vectơ \(\vec a\) và \(\vec b\).
Tích có hướng của hai vectơ \(\vec a\) và \(\vec b\) là
\(\left[ {\vec a,\vec b} \right] = \left( {1.0 - 1.\left( { - 2} \right);1.1 - 2.0;2.\left( { - 2} \right) - 1.1} \right) = \left( {2;1; - 5} \right)\).
Do đó, vectơ \(\vec n\) cần tìm là \(\vec n = \left( {2;1; - 5} \right)\).
(Trả lời bởi datcoder)
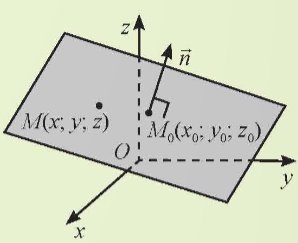
Trong không gian Oxyz, cho mặt phẳng (α) đi qua điểm M0(1; 2; 3) và nhận \(\overrightarrow{n}\) = (7; 5; 2) làm vectơ pháp tuyến. Gọi M(x; y; z) là một điểm tùy ý trong không gian. Tính tích vô hướng \(\overrightarrow{n}.\overrightarrow{M_0M}\) theo x, y, z.
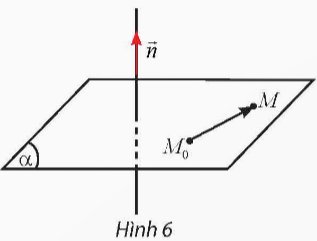
Thảo luận (1)Hướng dẫn giảiToạ độ của vectơ \(\overrightarrow {{M_0}M} \) là \(\left( {x - 1;y - 2;z - 3} \right)\)
Suy ra \(\vec n.\overrightarrow {{M_0}M} = 7\left( {x - 1} \right) + 5\left( {y - 2} \right) + 2\left( {z - 3} \right) = 7x + 5y + 2z - 23\)
(Trả lời bởi datcoder)
Cho hai mặt phẳng (α), (β) có phương trình tổng quát là (α): 2x + 2y – 3z – 4 = 0 và (β): x + 4z – 12 = 0.
a) Tìm một vectơ pháp tuyến của mỗi mặt phẳng (α), (β).
b) Tìm điểm thuộc mặt phẳng (α) trong số các điểm: M(1; 0; 1), N(1; 1; 0).
Thảo luận (1)Hướng dẫn giảia) Phương trình mặt phẳng \(\left( \alpha \right)\) là \(2x + 2y - 3z - 4 = 0\) nên \(\left( \alpha \right)\) nhận \(\overrightarrow {{n_{\left( \alpha \right)}}} = \left( {2;2; - 3} \right)\) làm một vectơ pháp tuyến.
Phương trình mặt phẳng \(\left( \beta \right)\) là \(x + 4z - 12 = 0\) nên \(\left( \beta \right)\) nhận \(\overrightarrow {{n_{\left( \beta \right)}}} = \left( {1;0;4} \right)\) làm một vectơ pháp tuyến.
b) Thay điểm \(M\left( {1;0;1} \right)\) vào phương trình mặt phẳng \(\left( \alpha \right)\), ta được:
\(2.1 + 2.0 - 3.1 - 4 = - 5 \ne 0\).
Vậy điểm \(M\) không thuộc \(\left( \alpha \right)\).
Thay điểm \(N\left( {1;1;0} \right)\) vào phương trình mặt phẳng \(\left( \alpha \right)\), ta được:
\(2.1 + 2.1 - 3.0 - 4 = 0\).
Vậy điểm \(N\) thuộc \(\left( \alpha \right)\).
(Trả lời bởi datcoder)
Trong không gian Oxyz, cho mặt phẳng (α) đi qua điểm M0(x0; y0; z0) và nhận \(\overrightarrow{n}=\left(A;B;C\right)\) làm vectơ pháp tuyến. Gọi M(x; y; z) là một điểm tùy ý trong không gian.
a) Tìm tọa độ của \(\overrightarrow{M_0M}\).
b) Tính tích vô hướng của \(\overrightarrow{n}.\overrightarrow{M_0M}\).
c) Lập phương trình tổng quát của mặt phẳng (α).
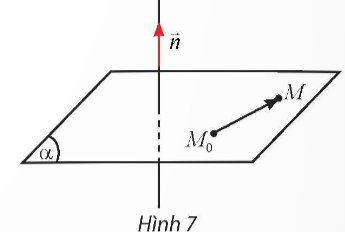
Thảo luận (1)Hướng dẫn giảia) Toạ độ của \(\overrightarrow {{M_0}M} \) là \(\left( {{x_M} - {x_{{M_0}}};{y_M} - {y_{{M_0}}};{z_M} - {z_{{M_0}}}} \right) = \left( {x - {x_0};y - {y_0};z - {z_0}} \right)\)
b) Ta có: \(\vec n.\overrightarrow {{M_0}M} = A\left( {x - {x_0}} \right) + B\left( {y - {y_0}} \right) + C\left( {z - {z_0}} \right)\)
c) Để lập được phương trình tổng quát của mặt phẳng \(\left( \alpha \right)\), điểm \(M\left( {x,y,z} \right)\) được chọn phải nằm trên \(\left( \alpha \right)\), điều này có nghĩa là \(\vec n.\overrightarrow {{M_0}M} = 0\).
Suy ra \(A\left( {x - {x_0}} \right) + B\left( {y - {y_0}} \right) + C\left( {z - {z_0}} \right) = 0\)
Vậy phương trình mặt phẳng \(\left( \alpha \right)\) là \(A\left( {x - {x_0}} \right) + B\left( {y - {y_0}} \right) + C\left( {z - {z_0}} \right) = 0\)
(Trả lời bởi datcoder)