a) Cho vectơ \(\overrightarrow{n}\) khác \(\overrightarrow{0}\). Qua một điểm M0 cố định trong không gian, có bao nhiêu mặt phẳng (α) vuông góc với giá của vectơ \(\overrightarrow{n}\)?
b) Cho hai vectơ \(\overrightarrow{a},\overrightarrow{b}\) không cùng phương. Qua một điểm M0 cố định trong không gian, có bao nhiêu mặt phẳng (α) song song hoặc chứa giá của hai vectơ \(\overrightarrow{a},\overrightarrow{b}\)?
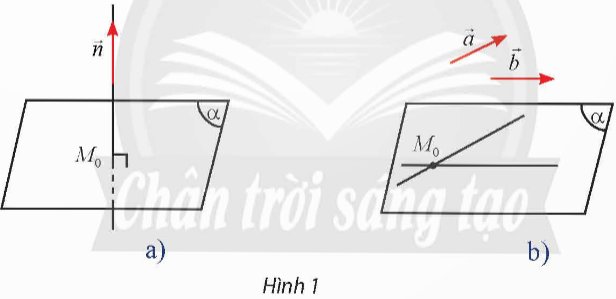
a) Với một điểm và một đường thẳng trong không gian, có duy nhất một mặt phẳng đi qua điểm và vuông góc với đường thẳng đó. Vậy có duy nhất một mặt phẳng \(\left( \alpha \right)\) đi qua điểm \({M_0}\) và vuông góc với giá của vectơ \(\vec n\).
b) Do hai vectơ \(\vec a\) và \(\vec b\) không cùng phương, giá của hai vectơ (lần lượt là \(a\) và \(b\)) không song song hay trùng nhau. Chọn đường thẳng \(a'\) sao cho \(a'\) song song hoặc trùng với \(a\) và \(a'\) cắt \(b\). Khi đó, có duy nhất một mặt phẳng \(\left( \beta \right)\) chứa \(a'\) và \(b\).
Nếu \({M_0} \in \left( \beta \right)\) thì mặt phẳng \(\left( \beta \right)\) là mặt phẳng duy nhất đi qua \({M_0}\) và song song hoặc chứa giá của hai vectơ \(\vec a\) và \(\vec b\).
Nếu \({M_0} \notin \left( \beta \right)\), thì trong không gian, tồn tại duy nhất mặt phẳng \(\left( \alpha \right)\) đi qua \({M_0}\) và song song với \(\left( \beta \right)\). Khi đó, \(\left( \alpha \right)\) song song hoặc chứa giá của hai vectơ \(\vec a\) và \(\vec b\).


