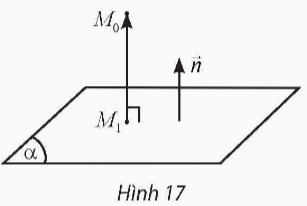
Trong không gian $O x y z$, cho mặt phẳng (a) có phương trình $\mathrm{Ax}+\mathrm{By}+\mathrm{Cz}+\mathrm{D}=0$ và điểm $\mathrm{M}_0\left(\mathrm{x}_0 ; \mathrm{y}_0 ; \mathrm{z}_0\right)$. Gọi $\mathrm{M}_1\left(\mathrm{x}_1 ; \mathrm{y}_1 ; \mathrm{z}_1\right)$ là hình chiếu vuông góc của $\mathrm{M}_0$ trên (a) (Hình 17).
a) Nêu nhận xét về phương của hai vectơ $\overrightarrow{M_1 M_0}=\left(x_0-x_1 ; y_0-y_1 ; z_0-z_1\right)$ và $\vec{n}=(A ; B ; C)$.
b) Tính $\overrightarrow{M_1 M_0} \cdot \vec{n}$ theo $\mathrm{A}, \mathrm{B}, \mathrm{C}, \mathrm{D}$ và tọa độ của $\mathrm{M}_0$.
c) Giải thích tại sao ta lại có đẳng thức $\left|\overrightarrow{M_1 M_0}\right| \cdot|\vec{n}|=\left|\overrightarrow{M_1 M_0} \cdot \vec{n}\right|$.
d) Từ các kết quả trên suy ra cách tính $d\left(M_0,(\alpha)\right)=\left|\overrightarrow{M_1 M_0}\right|=\frac{\left|\overrightarrow{M_1 M_0} \cdot \vec{n}\right|}{|\vec{n}|}$.