Trong không gian $O x y z$, cho mặt phẳng (a) có phương trình $\mathrm{Ax}+\mathrm{By}+\mathrm{Cz}+\mathrm{D}=0$ và điểm $\mathrm{M}_0\left(\mathrm{x}_0 ; \mathrm{y}_0 ; \mathrm{z}_0\right)$. Gọi $\mathrm{M}_1\left(\mathrm{x}_1 ; \mathrm{y}_1 ; \mathrm{z}_1\right)$ là hình chiếu vuông góc của $\mathrm{M}_0$ trên (a) (Hình 17).
a) Nêu nhận xét về phương của hai vectơ $\overrightarrow{M_1 M_0}=\left(x_0-x_1 ; y_0-y_1 ; z_0-z_1\right)$ và $\vec{n}=(A ; B ; C)$.
b) Tính $\overrightarrow{M_1 M_0} \cdot \vec{n}$ theo $\mathrm{A}, \mathrm{B}, \mathrm{C}, \mathrm{D}$ và tọa độ của $\mathrm{M}_0$.
c) Giải thích tại sao ta lại có đẳng thức $\left|\overrightarrow{M_1 M_0}\right| \cdot|\vec{n}|=\left|\overrightarrow{M_1 M_0} \cdot \vec{n}\right|$.
d) Từ các kết quả trên suy ra cách tính $d\left(M_0,(\alpha)\right)=\left|\overrightarrow{M_1 M_0}\right|=\frac{\left|\overrightarrow{M_1 M_0} \cdot \vec{n}\right|}{|\vec{n}|}$.
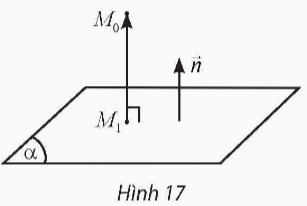
a) Vectơ pháp tuyến \(\vec n\) có giá vuông góc với \(\left( \alpha \right)\). Do \({M_1}\) là hình chiếu của \({M_0}\) trên \(\left( \alpha \right)\) nên \({M_1}{M_0} \bot \left( \alpha \right)\), suy ra \(\overrightarrow {{M_1}{M_0}} \) có giá vuông góc với \(\left( \alpha \right)\).
Hai vectơ \(\overrightarrow {{M_1}{M_0}} \) và \(\vec n\) cùng có giá vuông góc với \(\left( \alpha \right)\), nên chúng là hai vectơ cùng phương.
b) Ta có:
\(\overrightarrow {{M_1}{M_0}} .\vec n = A\left( {{x_0} - {x_1}} \right) + B\left( {{y_0} - {y_1}} \right) + C\left( {{z_0} - {z_1}} \right) = A{x_0} + B{y_0} + C{z_0} - \left( {A{x_1} + B{y_1} + C{z_1}} \right)\)
Do \({M_1} \in \left( \alpha \right)\) nên \(A{x_1} + B{y_1} + C{z_1} + D = 0 \Rightarrow D = - \left( {A{x_1} + B{y_1} + C{z_1}} \right)\).
Như vậy \(\overrightarrow {{M_1}{M_0}} .\vec n = A{x_0} + B{y_0} + C{z_0} + D\).
c) Ta có \(\overrightarrow {{M_1}{M_0}} .\vec n = \left| {\overrightarrow {{M_1}{M_0}} } \right|.\left| {\vec n} \right|.\cos \left( {\overrightarrow {{M_1}{M_0}} ,\vec n} \right)\).
Do \(\overrightarrow {{M_1}{M_0}} \) và \(\vec n\) cùng phương, nên góc giữa hai vectơ này bằng \({0^o}\) (cùng chiều) hoặc \({180^o}\) (ngược chiều).
Dễ thấy rằng \(\cos {0^o} = 1\) và \(\cos {180^o} = - 1\). Suy ra \(\left| {\cos {0^o}} \right| = \left| {\cos {{180}^o}} \right| = 1\), điều này có nghĩa là \(\left| {\cos \left( {\overrightarrow {{M_1}{M_0}} ,\vec n} \right)} \right| = 1\).
Như vậy, \[\left| {\overrightarrow {{M_1}{M_0}} .\vec n} \right| = \left| {\overrightarrow {{M_1}{M_0}} } \right|.\left| {\vec n} \right|.\left| {\cos \left( {\overrightarrow {{M_1}{M_0}} ,\vec n} \right)} \right| = \left| {\overrightarrow {{M_1}{M_0}} } \right|.\left| {\vec n} \right|\].
d) Ta có \({M_1}{M_0} \bot \left( \alpha \right)\) và \({M_1} \in \left( \alpha \right)\) nên khoảng cách từ \({M_0}\) đến mặt phẳng \(\left( \alpha \right)\) là đoạn thẳng \({M_1}{M_0}\). Suy ra \(\left| {\overrightarrow {{M_1}{M_0}} } \right| = {M_1}{M_0} = d\left( {{M_0},\left( \alpha \right)} \right)\).
Vậy ta có \(d\left( {{M_0},\left( \alpha \right)} \right) = \left| {\overrightarrow {{M_1}{M_0}} } \right| = \frac{{\left| {\overrightarrow {{M_1}{M_0}} .\vec n} \right|}}{{\left| {\vec n} \right|}}\).


