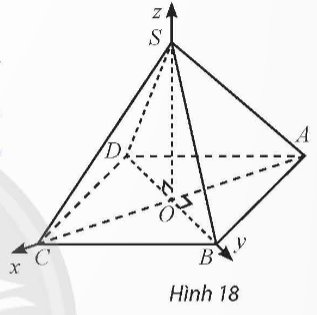
Hình vuông \(ABCD\) có cạnh \(a\sqrt 2 \), nên đường chéo có độ dài \(\sqrt {{{\left( {a\sqrt 2 } \right)}^2} + {{\left( {a\sqrt 2 } \right)}^2}} = 2a\). Suy ra \(OA = OB = OC = \frac{{2a}}{2} = a\).
Chiều cao của hình chóp đều là \(2a\), nên \(SO = 2a\)
Điểm \(A\) nằm trên trục \(Ox\), \(OA = a\) và \({x_A} < 0\) nên ta có \(A\left( { - a;0;0} \right)\).
Điểm \(B\) nằm trên trục \(Oy\), \(OB = a\) và \({y_B} > 0\) nên ta có \(B\left( {0;a;0} \right)\).
Điểm \(C\) nằm trên trục \(Ox\), \(OC = a\) và \({x_C} > 0\) nên ta có \(C\left( {a;0;0} \right)\).
Điểm \(S\) nằm trên trục \(Oz\), \(OS = 2a\) và \({z_S} > 0\) nên ta có \(S\left( {0;0;2a} \right)\).
Mặt phẳng \(\left( {SAB} \right)\) đi qua \(A\left( { - a;0;0} \right)\), \(B\left( {0;a;0} \right)\), \(S\left( {0;0;2a} \right)\) nên có phương trình là \(\frac{x}{{ - a}} + \frac{y}{a} + \frac{z}{{2a}} = 1 \Leftrightarrow - 2x + 2y + z = 2a \Leftrightarrow - 2x + 2y + z - 2a = 0\).
Khoảng cách từ \(C\left( {a;0;0} \right)\) đến mặt phẳng \(\left( {SAB} \right)\) là:
\(d\left( {C,\left( {SAB} \right)} \right) = \frac{{\left| { - 2.a + 2.0 + 0 - 2a} \right|}}{{\sqrt {{{\left( { - 2} \right)}^2} + {2^2} + {1^2}} }} = \frac{{4a}}{3}\)