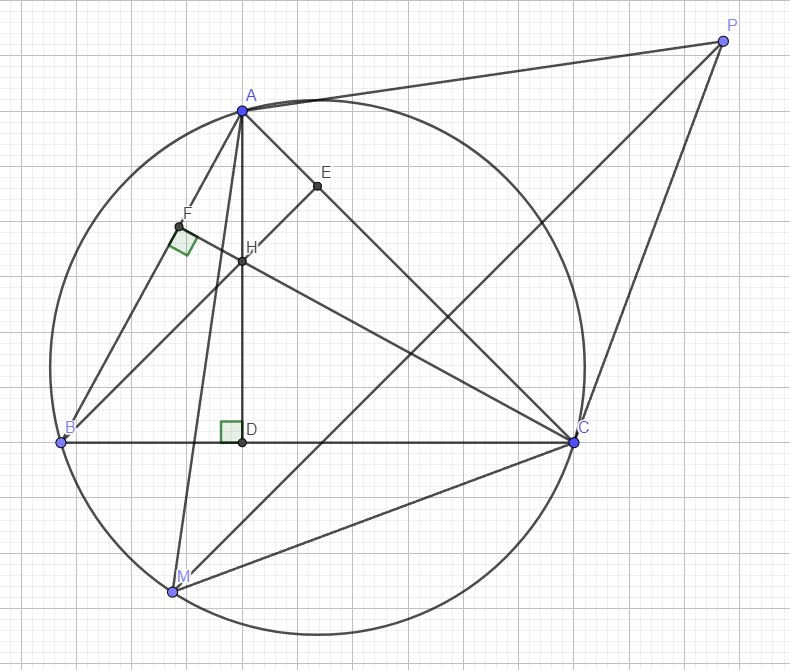
Cho tam giác abc nhọn nội tiếp đường tròn tâm O. Hai đường cao BE, CF của tam giác ABC cắt nhau tại H. Gọi D là giao đểm của AH và BC
a) Chứng minh tứ giác BFEC nội tiếp đường tròn và OA ⊥ EF
b) Vẽ đường kính AK của (O).CHứng minh AB.KC=Ak.BD suy ra AB.KC+AC.KB=AK.BC