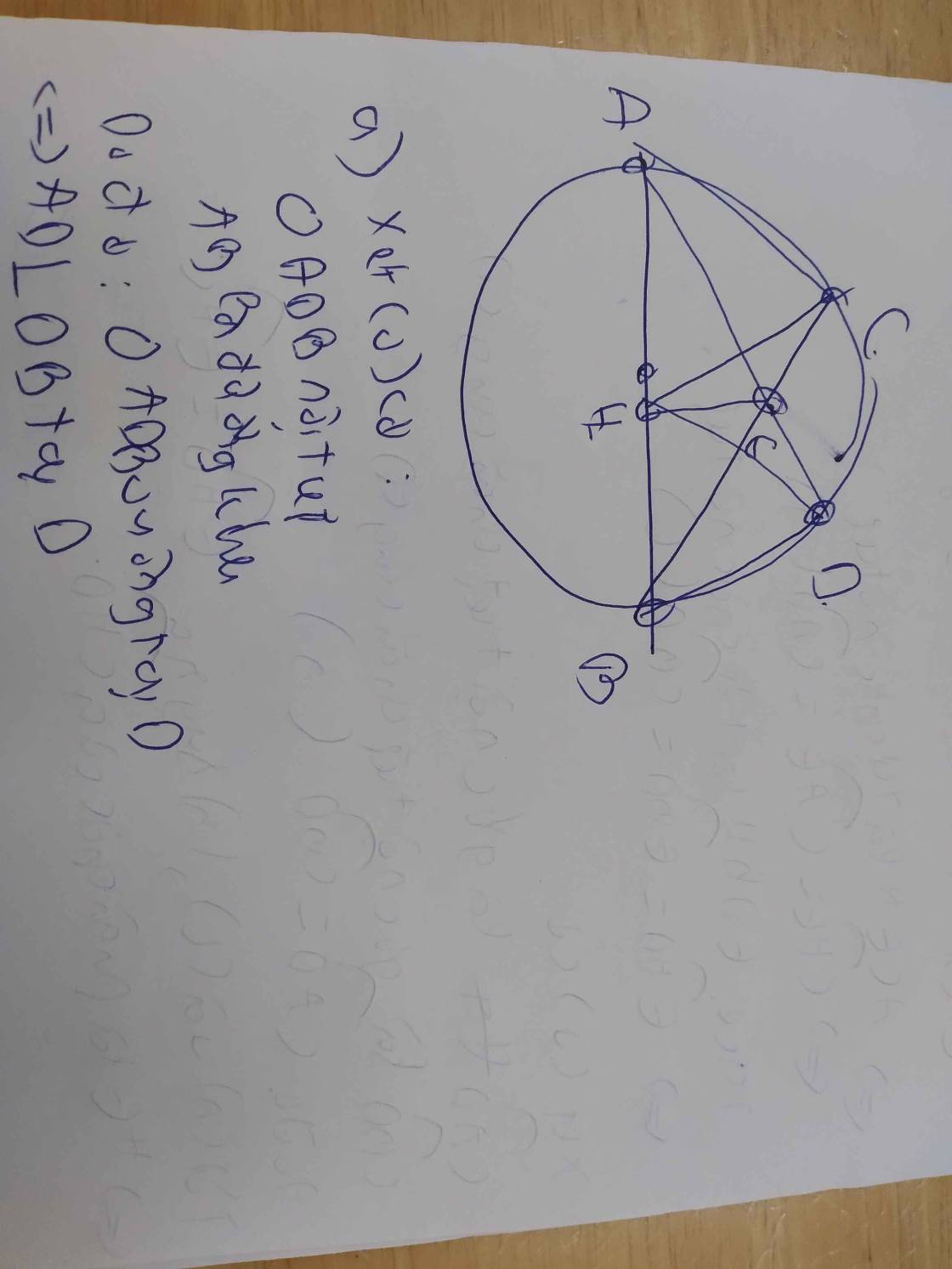
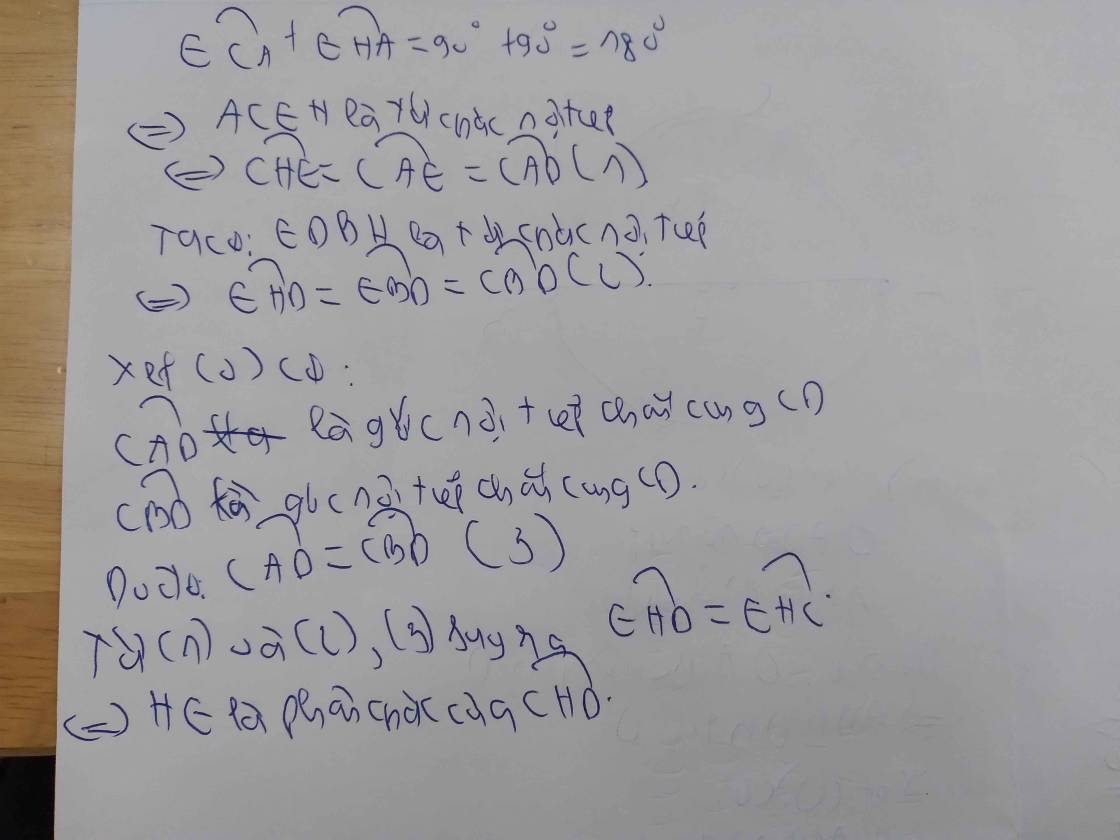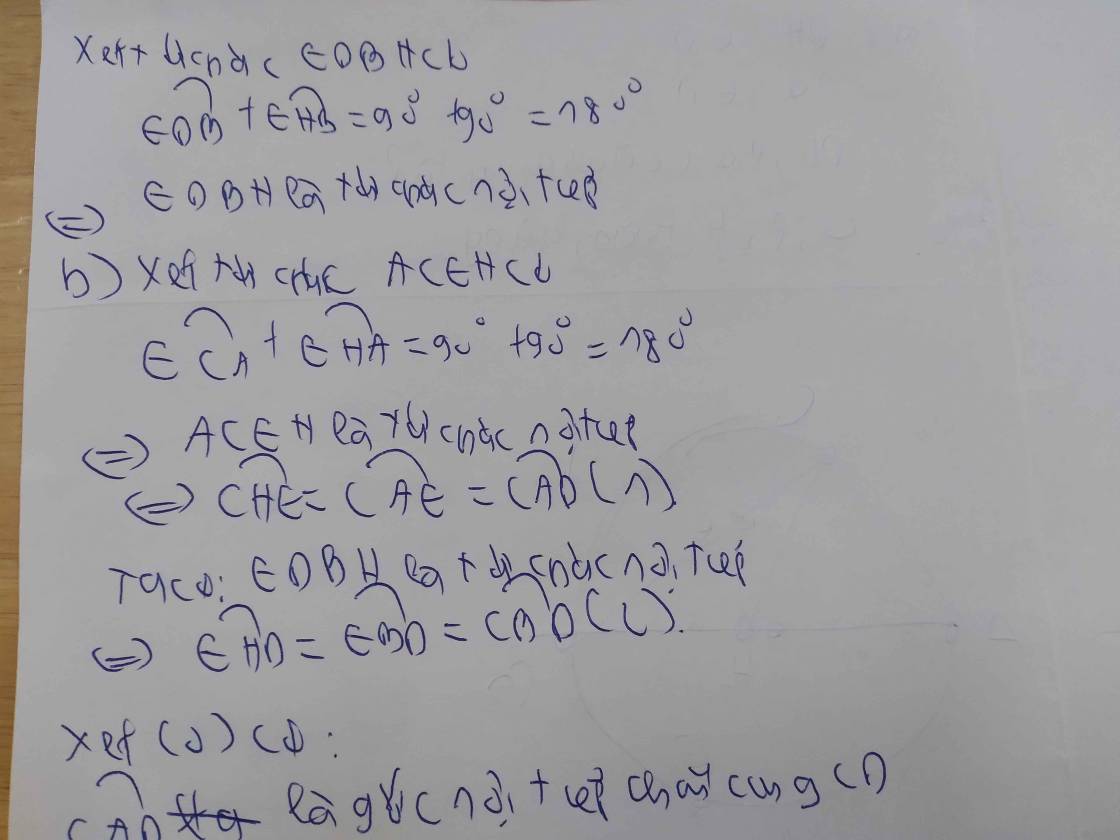Cho tam giac abc nội tiếp đường tròn tâm O. 2 đừng cao BD CE cất nhau tại H.
a) Cm 4 điểm B D C E cùng nằm trên 1 đường tròn.
b) DE vuông gọc vói OA.
c)M,N là trung điểm BC, AH. K là giao điểm OM, CE. L là giao điểm MN BD. Cm: KL//AC
Ghi cách chứng minh thôi. Đang cần câu c ạ.
cho tam giác ABC có ba góc nhọn,vẽ hai đường cao BE và CF cắt nhau tại H
a) Chứng minh AH vuông góc BC.
b)Chứng minh bốn điểm B,C,E,F cùng thuộc đường tròn
cái bài mình bấm sai đấy không phải bài 7 đâu
Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Trên tia đối của tia AB lấy điểm M. Qua M kẻ đường thẳng (d) cắt (O) tại C và D (C nằm giữa M và D), đường thẳng (d') cắt (O') tại E và F (E nằm giữa F và M). Chứng minh CDFE là tứ giác nội tiếp
Xét tứ giác ACDB có A,C,D,B cùng nằm trên (O)
nên ACDB là tứ giác nội tiếp
=>\(\widehat{CAB}+\widehat{CDB}=180^0\)
mà \(\widehat{CAB}+\widehat{MAC}=180^0\)(hai góc kề bù)
nên \(\widehat{MAC}=\widehat{CDB}=\widehat{MDB}\)
Xét tứ giác AEFB có A,E,F,B cùng nằm trên (O')
nên AEFB là tứ giác nội tiếp
=>\(\widehat{BAE}+\widehat{BFE}=180^0\)
mà \(\widehat{BAE}+\widehat{MAE}=180^0\)(hai góc kề bù)
nên \(\widehat{MAE}=\widehat{MFB}\)
Xét ΔMCA và ΔMBD có
\(\widehat{MAC}=\widehat{MDB}\)
\(\widehat{M}\) chung
Do đó: ΔMCA đồng dạng với ΔMBD
=>\(\dfrac{MC}{MB}=\dfrac{MA}{MD}\)
=>\(MC\cdot MD=MA\cdot MB\)(1)
Xét ΔMAE và ΔMFB có
\(\widehat{MAE}=\widehat{MFB}\)
\(\widehat{M}\) chung
Do đó: ΔMAE đồng dạng với ΔMFB
=>\(\dfrac{MA}{MF}=\dfrac{ME}{MB}\)
=>\(MA\cdot MB=MF\cdot ME\left(2\right)\)
Từ (1) và (2) suy ra \(MC\cdot MD=ME\cdot MF\)
=>\(\dfrac{MC}{MF}=\dfrac{ME}{MD}\)
Xét ΔMCE và ΔMFD có
\(\dfrac{MC}{MF}=\dfrac{ME}{MD}\)
\(\widehat{CME}\) chung
Do đó: ΔMCE đồng dạng với ΔMFD
=>\(\widehat{MCE}=\widehat{MFD}\)
mà \(\widehat{MCE}+\widehat{DCE}=180^0\)(hai góc kề bù)
nên \(\widehat{MFD}+\widehat{DCE}=180^0\)
=>CDFE là tứ giác nội tiếp
Câu 8 (2,5 điểm). Trên đường tròn (O) đường kính AB = 2R lấy di*k_{m}*C sao cho AC = R và lấy điểm D bất kì trên cung nhỏ BC (D khác C và B). Gọi E là giao điểm của AD và BC, H là hình chiếu của E trên AB. a) Chứng minh tứ giác EDBH là tứ giác nội tiếp. b) Chứng minh HE là tia phân giác của góc CHD. c) Xác định vị trí của điểm D để chu vị tử giác ABDC lớn nhất.
Di*k_{m}*C là điểm C nhó vì do bị lỗi phông chữ mong mng thông cảm vs ạ🥺
thầy cô giúp e với ạ
Đương nhiên là đường phân giác, vì khi kẻ 2 đường vuông góc sẽ tạo ra 2 tam giác vuông. Để 2 tam giác vuông đồng dạng chúng cần thêm 1 cặp góc bằng nhau khác, và luôn có thể tạo ra cặp góc bằng nhau từ 1 đường phân giác.
Bài 8. Cho tam giác ABC. Dựng ngoài tam giác đó các tam giác đều BCD, ACE, ABF. Chứng minh rằng:
a) Ba đường tròn ngoại tiếp tam giác đều nói trên đều đi qua 1 điểm
b) Ba đường thẳng AD, BE,CF bằng nhau
c) Ba đoạn thẳng AD,BE,CF bằng nhau
cho tứ giác ABCD nội tiếp đường tròn O, hai đường chéo AC và BD cắt nhau tại I. Vẽ đường tròn ngoại tiếp tam giác ABI. Tiếp tuyến của đường tròn này tại I cắt AC và AD lần lượt tại M và N. Chứng minh rằng:
a) MN//Cd
b) ABNM nội tiếp
Cho đường tròn (O), dây AB. Các tiếp tuyến của đường tròn tại A và B cắt nha tại C. Trên dây AB lấy điểm E(EA>EB). Đường vuông góc với OE tại E cắt CA và CB theo thứ tự ở I và K. Chứng minh rằng
1) OAEI, OEBK là các tứ giác nội tiếp 3) AI = BK
2) OIK là tam giác cân 4) OICK là tứ giác nội tiếp
1: Xét tứ giác OAEI có \(\widehat{OAI}+\widehat{OEI}=90^0+90^0=180^0\)
nên OAEI là tứ giác nội tiếp
Xét tứ giác OEBK có \(\widehat{OEK}=\widehat{OBK}=90^0\)
nên OEBK là tứ giác nội tiếp
2: Ta có: OAEI là tứ giác nội tiếp
=>\(\widehat{OIE}=\widehat{OAE}=\widehat{OAB}\left(1\right)\)
Ta có: OEBK là tứ giác nội tiếp
=>\(\widehat{OKE}=\widehat{OBE}=\widehat{OBA}\left(2\right)\)
Ta có: ΔOAB cân tại O
=>\(\widehat{OAB}=\widehat{OBA}\left(3\right)\)
Từ (1),(2),(3) suy ra \(\widehat{OIE}=\widehat{OKE}\)
=>\(\widehat{OIK}=\widehat{OKI}\)
=>ΔOKI cân tại O
3: Xét ΔOAI vuông tại A và ΔOBK vuông tại B có
OA=OB
OI=OK
Do đó: ΔOAI=ΔOBK
=>AI=BK
4: Xét tứ giác OACB có \(\widehat{OAC}+\widehat{OBC}=90^0+90^0=180^0\)
nên OACB là tứ giác nội tiếp
=>\(\widehat{OAB}=\widehat{OCB}\)
mà \(\widehat{OAB}=\widehat{OIK}\)
nên \(\widehat{OIK}=\widehat{OCK}\)
=>OICK là tứ giác nội tiếp
2. Cho đường thẳng d cố định cắt đường tròn (O;R) tại hai điểm phân biệt C, DCD khác đường kính). Trên tia đối của tia CD lấy điểm M. Kẻ hai tiếp tuyến MA, MB (A, B là tiếp điểm) với đường tròn (O) (tia MC nằm giữa hai tia MA, MO). Gọi H là giao điểm của AB và OM.
a) Kẻ đường kính AE của đường tròn (O). EC, ED cắt đường thẳng OM lần lượt tại G và I. Gọi K là giao điểm của AG với (O). Chứng minh OG = OI và ba điểm K, O, D
thẳng hàng.
b) Đường thẳng đi qua O và vuông góc với OM cắt các tia MA, MB lần lượt tại P, Q. Tìm vị trí của điểm M trên đường thẳng d để diện tích tam giác MPQ đạt giá trị nhỏ nhất.
Cho tứ giác ABCD nội tiếp đường tròn đường kính AD.Hai đường chéo AC và BD cắt nhau tại E.Kẻ EF vuông góc với AD.Gọi M là trung điểm của DE.Chứng minh:
a)Các tứ giác ABEF,DCEF nội tiếp
b)tia CA là tia phân giác của góc BCF
giup minh voii
a: Xét (O) có
ΔABD nội tiếp
AD là đường kính
Do đó: ΔADB vuông tại B
Xét (O) có
ΔACD nội tiếp
AD là đường kính
Do đó: ΔACD vuông tại C
Xét tứ giác ABEF có \(\widehat{ABE}+\widehat{AFE}=90^0+90^0=180^0\)
nên ABEF là tứ giác nội tiếp
Xét tứ giác DCEF có \(\widehat{DCE}+\widehat{DFE}=90^0+90^0=180^0\)
nên DCEF là tứ giác nội tiếp
b: Ta có: DCEF là tứ giác nội tiếp
=>\(\widehat{FCE}=\widehat{FDE}\)
=>\(\widehat{FCA}=\widehat{BDA}\left(1\right)\)
Xét (O) có
\(\widehat{BCA}\) là góc nội tiếp chắn cung BA
\(\widehat{BDA}\) là góc nội tiếp chắn cung BA
Do đó: \(\widehat{BCA}=\widehat{BDA}\left(2\right)\)
Từ (1),(2) suy ra \(\widehat{BCA}=\widehat{FCA}\)
=>CA là phân giác của góc BCF
