
giúp em câu 3, với ạ

giúp em câu 3, với ạ
3: MD^2=MI*MA
=>MD/MA=MI/MD
=>ΔMDI đồng dạng với ΔMAD
=>góc MDI=góc MAD
DNIC nội tiếp
=>góc NDI=góc NCI
=>góc MAD=góc NCI
=>góc NCI=góc KCI
=>C,K,N thẳng hàng

giúp em câu c với ạ
c: AH//OC
=>góc MAE=góc ACB=góc AFE
Xét ΔMAE và ΔMFA có
góc MAE=góc MFA
góc AME chung
=>ΔMAE đồng dạng với ΔMFA
=>MA^2=ME*MF
ΔTAM vuông tại A có KA vuông góc TM
nên MA^2=MK*MT=ME*MF
=>MK/MF=ME/MT
=>ΔMKE đồng dạng với ΔMFT
=>góc MKE=góc MFT
=>EFTK nội tiếp
mà góc AKI=góc ATI=90 độ
nên EFTK nội tiếp đường tròn đường kính AI
=>góc IAE=góc IKE=góc MKE
=>góc IAE=góc TFE
góc IAE=góc EBA
=>góc TFE=góc ABE=góc FBE
BCEF nội tiế dfdường tròn tâm N đường kính BC
=>NE=NF
=>góc FBE=1/2*sđ cung EF=1/2*góc ENF
=>góc TFE=1/2(180 độ-2*góc NFE)
=>góc TFE=90d dộ-góc NFE
=>góc TFN=90 độ
=>góc NFC+góc TFC=90 độ
mà NF=NC
nên ΔNFC cân tại N
=>góc NFC=góc NCF
ΔCHD vuông tại D
=>góc NCF+góc CHD=90 độ
=>góc TFC=góc CHD
mà góc THF=góc CHD
nên góc TFC=góc THF
=>ΔTHF cân tại T
=>TF=TH=TA
=>ĐPCM

giúp em câu c vs ạ
c: góc MCK=góc MAC
góc NAE=góc MCI
=>góc MCK=góc MCI
Chứng minh tương tự, ta được: góc MBK=góc MBI
=>I đối xứng K qua BC

giúp em câu c với ạ

câu c làm như thế nào v ạ
3: Gọi I là điểm đối xứng của O qua BC, OI cắt BC tại N
=>N là trung điểm chung của OI và BC và I,N cố định
BH//CD; CH//BD
=>BHCD là hbh
=>N là trung điểm của HD
ON là đường trung bình của ΔAHD
=>AH=2ON
=>AH=OI=2ON
AH//OI
=>AHOI là hbh
=>IH=OA=R
=>H thuộc (I;R) cố định
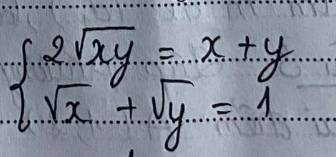
pt này giải ntn vậy ạ
\(\Leftrightarrow\left\{{}\begin{matrix}\left(\sqrt{x}-\sqrt{y}\right)^2=0\\\sqrt{x}+\sqrt{y}=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\sqrt{x}-\sqrt{y}=0\\\sqrt{x}+\sqrt{y}=1\end{matrix}\right.\)
\(\Rightarrow2\sqrt{x}=1\Rightarrow x=\left(\dfrac{1}{2}\right)^2=\dfrac{1}{4}\)
\(\Rightarrow y=\dfrac{1}{4}\)
Vậy hệ phương trình có tập nghiệm \(S=\left(\dfrac{1}{4};\dfrac{1}{4}\right)\)

câu d, làm ntn v ạ
Bạn ơi chỉ mình câu c với đc kh ạ. Mình mới tìm ra góc ACD = góc AHE à, còn cái nào nữa để chứng mình đồng dạng v ạ

Câu 3.2 làm ntn v ạ, giúp em vs
3.2:
Theo vi ét: \(\left\{{}\begin{matrix}x_1+x_2=2m+2\\x_1x_2=m^2+m\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x_1+x_2\right)^2=\left(2m+2\right)^2=4m^2+8m+4\\4x_1x_2=4m^2+4m\end{matrix}\right.\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2=4m+4=2\left(2m+2\right)=2\left(x_1+x_2\right)\)
\(\Rightarrow\left(x_1+x_2\right)^2-4x_1x_2-2\left(x_1+x_2\right)=4m^2+8m+4-4m^2-4m-4m-4=0\)
Vậy hệ thức liên hệ giữa \(x_1\) và \(x_2\) mà không phụ thuộc vào tham số m là \(\left(x_1+x_2\right)^2-4x_1x_2-2\left(x_1+x_2\right)\)
2: x1+x2=2m+2; x1x2=m^2+m
(x1+x2)^2-4x1x2
=4m^2+8m+4-4m^2-4m=4m+4
=>(x1+x2)^2-4x1x2-2(x1+x2)=4m+4-4m-4=0 ko phụ thuộc m

làm giúp mình câu 2c vs ạ
Cho tam giác ABC cân tại A, đường cao AH, E là trung điểm của AH, M là hình chiếu vuông góc của H lên BE. Chứng minh AMHC là tứ giác nội tiếp. Mọi người giúp mình giải bài này với ạ