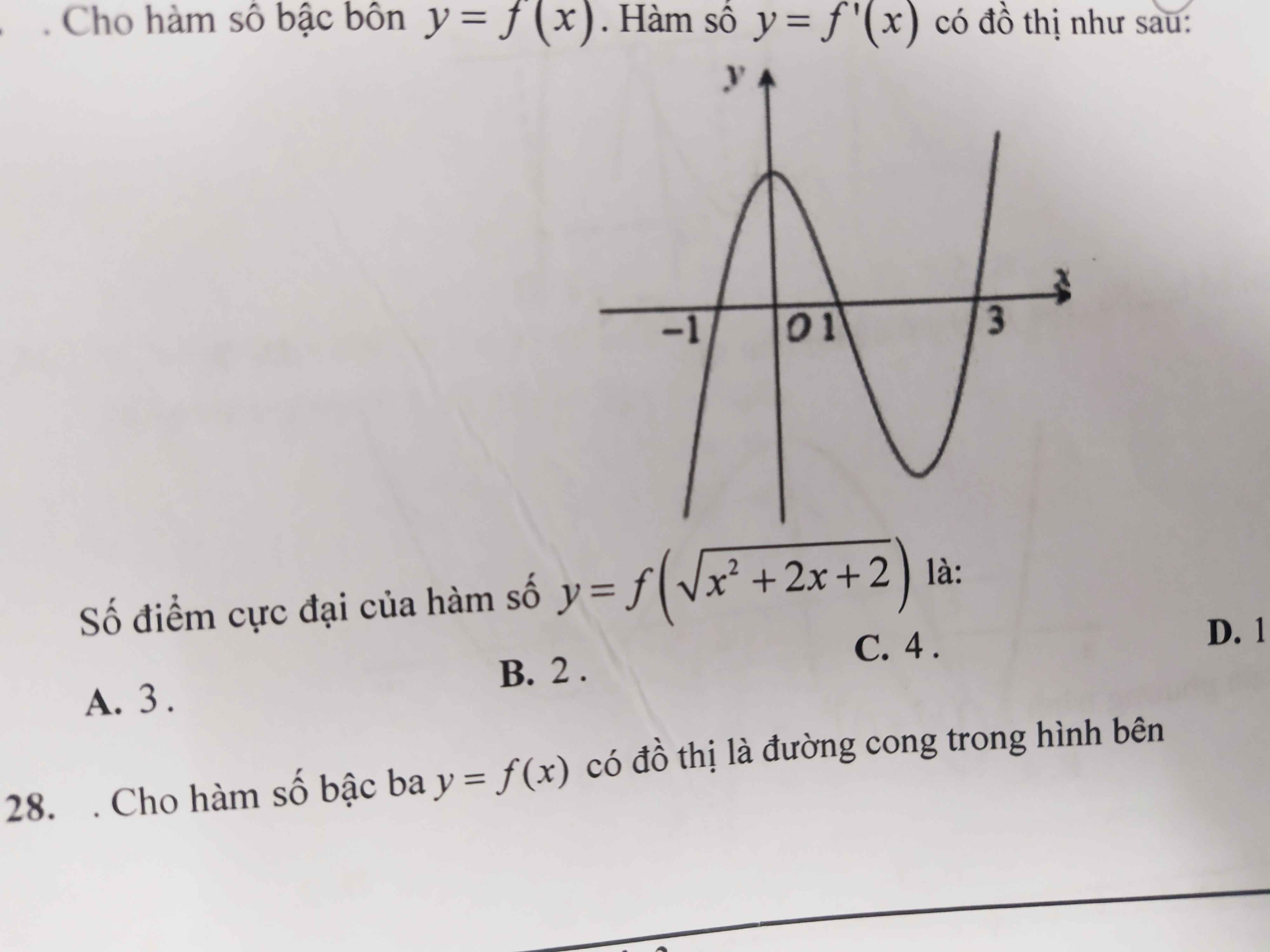log5 = a. Tính log\(\dfrac{1}{64}\) theo a
Bài 3: Lôgarit
6 tháng 8 2021 lúc 15:24
Ac giúp em với, cảm ơn trước ạ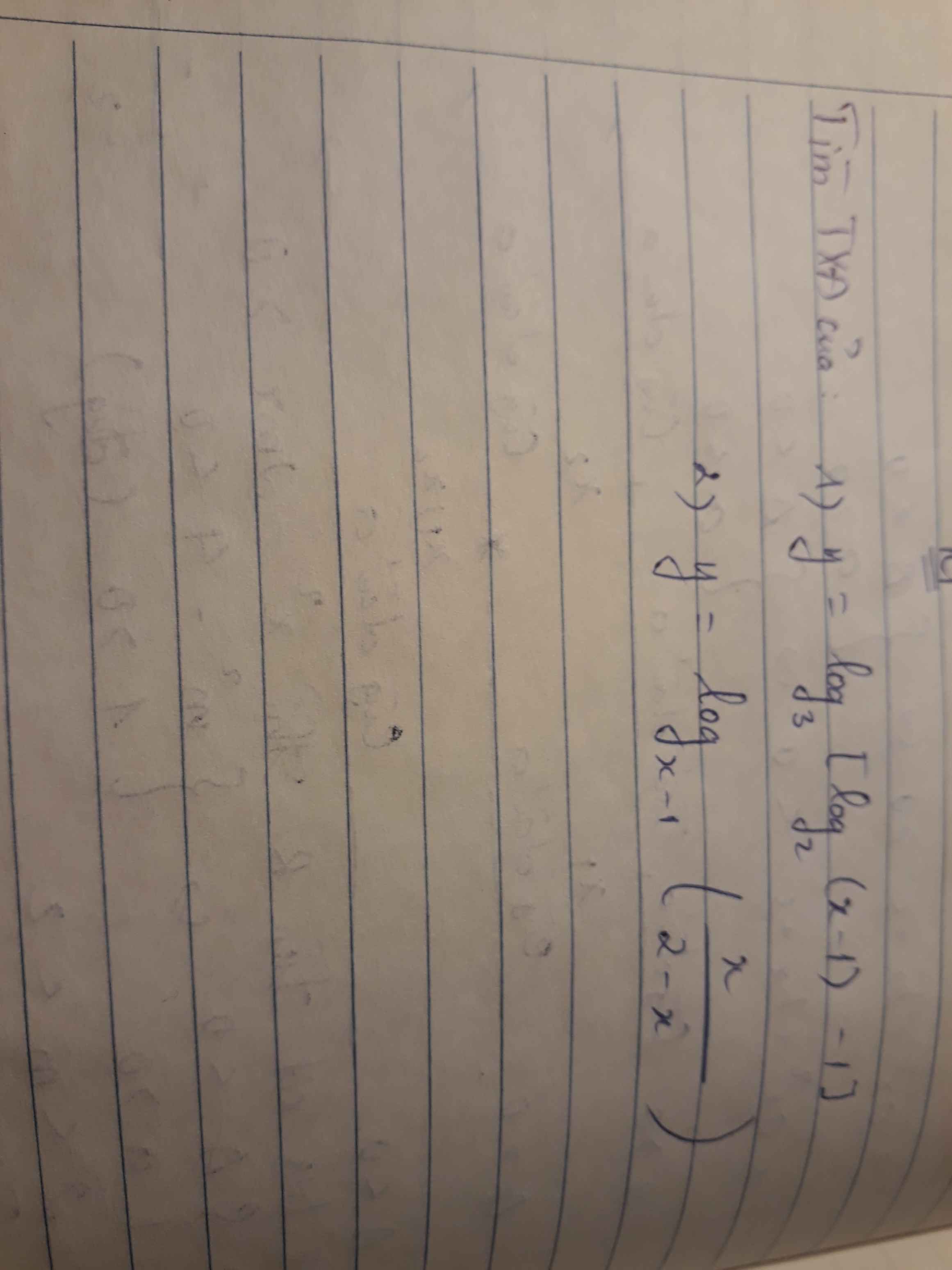
ĐKXĐ:
1.
\(\left\{{}\begin{matrix}x-1>0\\log_2\left(x-1\right)-1>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x>1\\x-1>2\end{matrix}\right.\) \(\Leftrightarrow x>3\)
2.
\(\left\{{}\begin{matrix}x-1>0\\x-1\ne1\\\dfrac{x}{2-x^2}>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x>1\\x\ne2\\\left[{}\begin{matrix}x< -\sqrt{2}\\0< x< \sqrt{2}\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow1< x< \sqrt{2}\)
Đúng 1
Bình luận (0)
7 tháng 8 2021 lúc 8:38
giải phương trình: \(4^x-5.2^x+4=0\)
Đặt \(2^x=t>0\) ta được:
\(t^2-5t+4=0\Rightarrow\left[{}\begin{matrix}t=1\\t=4\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}2^x=1\\2^x=4\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
Đúng 1
Bình luận (0)
9 tháng 8 2021 lúc 21:02
Hàm số y = log2( 4x- 2x+ m) có tập xác định D= R khi nào?
\(\Leftrightarrow4^x-2^x+m>0;\forall x\)
Đặt \(2^x=t>0\Rightarrow t^2-t+m>0;\forall t>0\)
\(\Rightarrow m>-t^2+t\Rightarrow m>\max\limits_{t>0}\left(-t^2+t\right)=\dfrac{1}{4}\)
Vậy \(m>\dfrac{1}{4}\)
Đúng 2
Bình luận (3)
\(y'=\left(2x-2\right)f'\left(x^2-2x\right)=0\Rightarrow\left\{{}\begin{matrix}x=1\\f'\left(x^2-2x\right)=0\end{matrix}\right.\)
Xét \(f'\left(x^2-2x\right)=0\Rightarrow\left\{{}\begin{matrix}x^2-2x=-2\\x^2-2x=1\\x^2-2x=3\end{matrix}\right.\)
\(\Rightarrow x=\left\{-1;1-\sqrt{2};1+\sqrt{2};3\right\}\)
Bảng xét dấu:
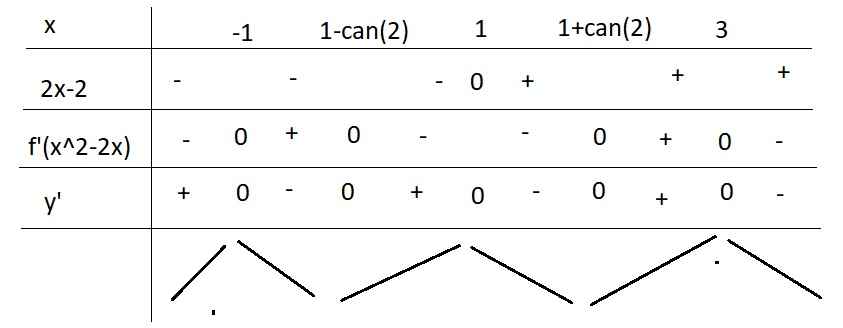
Hàm có 2 cực tiểu (sao khác cả 2 đáp án khoanh thế kia)
Đúng 0
Bình luận (5)
16 tháng 8 2021 lúc 21:40
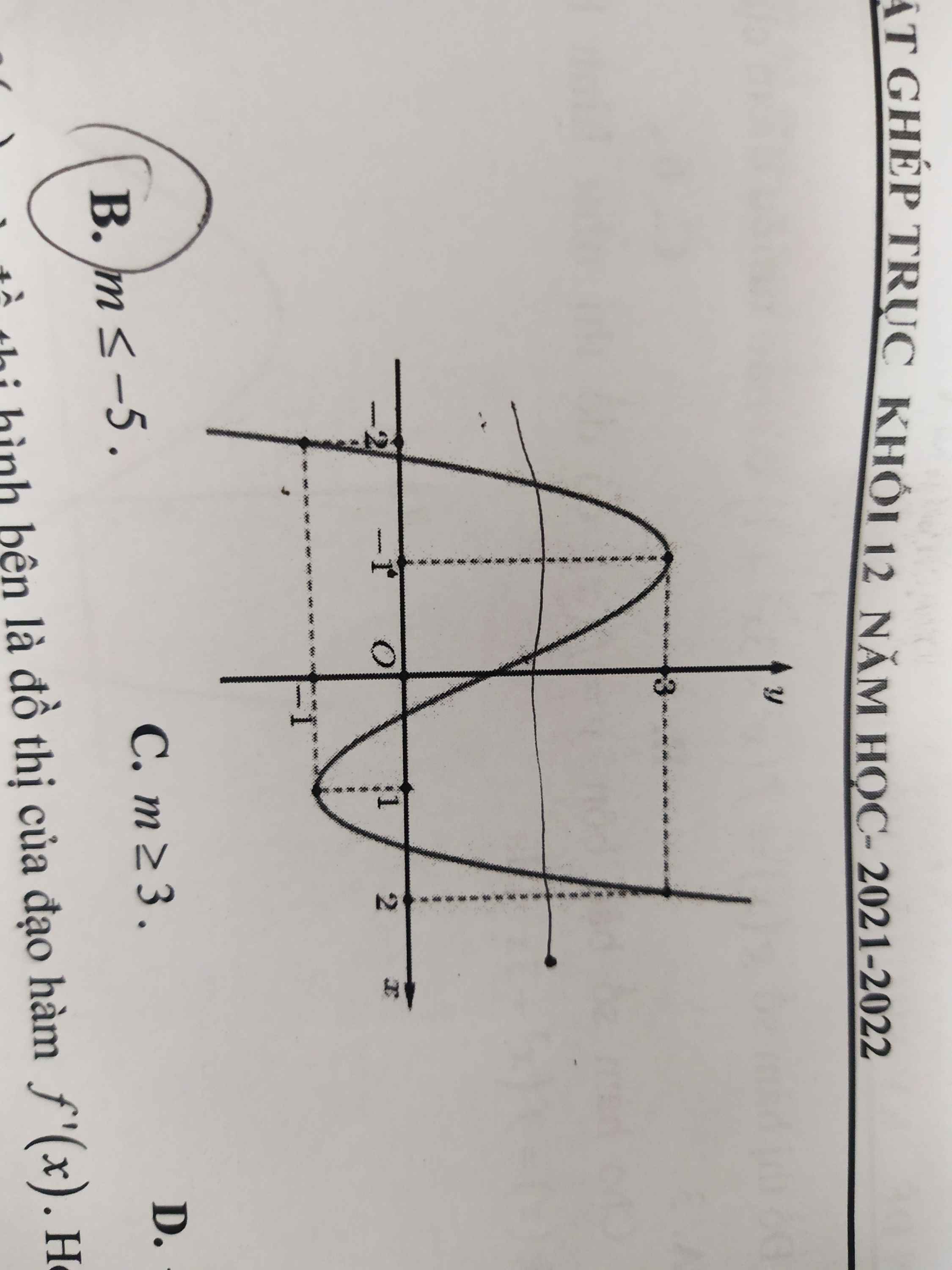
Cho hàm số y = f(x) liên tục trên R và có đồ thị như hình vẽ (dưới bình luận). Tìm tất cả các giá trị của tham số m để hàm số y= \(\left|f^2\left(x\right)-4f\left(x\right)+m\right|\) có 7 điểm cực trị (giải theo phương pháp ghép trục)
cho log23=a, log25=b. tính log\(\sqrt{10}\)30
\(log_{\sqrt{10}}30=\dfrac{log_230}{log_2\sqrt{10}}=\dfrac{log_22+log_23+log_25}{\dfrac{1}{2}\left(log_22+log_25\right)}=\dfrac{2\left(1+a+b\right)}{1+b}\)
Đúng 0
Bình luận (0)
Log 5 = bao nhieu va cach tinh. thank you
Cho Log 3 6 = a, Log 2 5 = b . Tính Log 10 90 theo a b
Mình cảm ơn ạ !
Tìm TXĐ:
a) y=\(\left(1-x\right)^{\dfrac{-1}{3}}\)
b) \(y=\sqrt{\log_{0,5}\dfrac{2x+1}{x+5}-2}\)
c) \(y=\log_{10}\sqrt{x^2-x-12}\)
d) \(y=\sqrt{\log_{10}x-1+\log_{10}x+1}\)
a: ĐKXĐ: 1-x>0
=>x<1
=>TXĐ là D=(-∞;1)
c: ĐKXĐ: \(x^2-x-12>0\)
=>\(x^2-4x+3x-12>0\)
=>(x-4)(x+3)>0
=>x>4 hoặc x<-3
Vậy: TXĐ là D=(4;+∞)\(\cup\) (-∞;-3)
b: ĐKXĐ: \(\frac{2x+1}{x+5}>0\) và \(\log_{0,5}\frac{2x+1}{x+5}-2\ge0\)
=>\(\left[\begin{array}{l}x>-\frac12\\ x<-5\end{array}\right.\) và \(\log_{0,5}\frac{2x+1}{x+5}\ge2\)
=>\(\left[\begin{array}{l}x>-\frac12\\ x<-5\end{array}\right.\) và \(\frac{2x+1}{x+5}\le\frac14\)
=>\(\left[\begin{array}{l}x>-\frac12\\ x<-5\end{array}\right.\) và \(\frac{2x+1}{x+5}-\frac14\le0\)
=>\(\left[\begin{array}{l}x>-\frac12\\ x<-5\end{array}\right.\) và \(\frac{4\left(2x+1\right)-\left(x+5\right)}{4\left(x+5\right)}\le0\)
=>\(\left[\begin{array}{l}x>-\frac12\\ x<-5\end{array}\right.\) và \(\frac{8x+4-x-5}{4\left(x+5\right)}\le0\)
=>\(\left[\begin{array}{l}x>-\frac12\\ x<-5\end{array}\right.\) và \(\frac{7x-1}{x+5}\le0\)
=>\(\left[\begin{array}{l}x>-\frac12\\ x<-5\end{array}\right.\) và \(-5
=>\(-\frac12
=>TXĐ là D=(-1/2;1/7]
Đúng 0
Bình luận (0)
Tính đạo hàm của hàm số sau:
a) \(y=ln\left(1+\sqrt{3x-1}\right)\)
b) \(y=log\left(2sin^2x-1\right)\)
c) \(y=3^{x^3+3x+1}e^x\)
a.
\(y'=\dfrac{\left(1+\sqrt{3x-1}\right)'}{1+\sqrt{3x-1}}=\dfrac{3}{2\left(1+\sqrt{3x-1}\right)\sqrt{3x-1}}\)
b.
\(y'=\dfrac{\left(2sin^2x-1\right)'}{\left(2sin^2x-1\right).ln10}=\dfrac{2sin2x}{\left(2sin^2x-1\right)ln10}\)
c.
\(y'=\left(3x^2+3\right)3^{x^3+3x+1}.e^x.ln3+3^{x^3+3x+1}.e^x\)
Đúng 0
Bình luận (0)