\(\Leftrightarrow4^x-2^x+m>0;\forall x\)
Đặt \(2^x=t>0\Rightarrow t^2-t+m>0;\forall t>0\)
\(\Rightarrow m>-t^2+t\Rightarrow m>\max\limits_{t>0}\left(-t^2+t\right)=\dfrac{1}{4}\)
Vậy \(m>\dfrac{1}{4}\)
\(y'=\left(2x-2\right)f'\left(x^2-2x\right)=0\Rightarrow\left\{{}\begin{matrix}x=1\\f'\left(x^2-2x\right)=0\end{matrix}\right.\)
Xét \(f'\left(x^2-2x\right)=0\Rightarrow\left\{{}\begin{matrix}x^2-2x=-2\\x^2-2x=1\\x^2-2x=3\end{matrix}\right.\)
\(\Rightarrow x=\left\{-1;1-\sqrt{2};1+\sqrt{2};3\right\}\)
Bảng xét dấu:
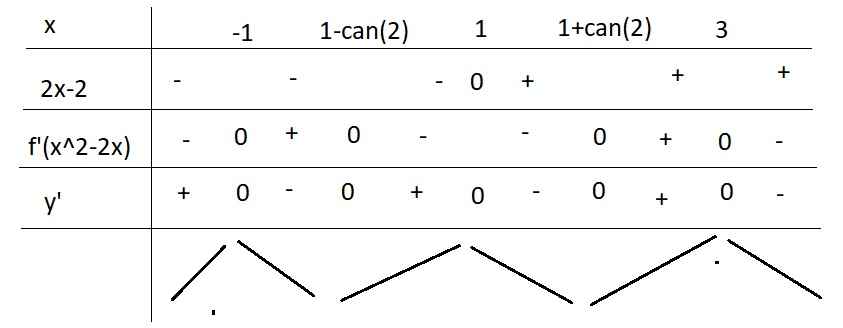
Hàm có 2 cực tiểu (sao khác cả 2 đáp án khoanh thế kia)












