Bài 2: Hệ hai phương trình bậc nhất hai ẩn. Luyện tập

Ptr hoành độ của `(P)` và `(d)` là:

       `x^2=-5x-3m+1`

`<=>x^2+5x+3m-1=0`   `(1)`

Để `(P)` cắt `(d)` tại `2` điểm phân biệt thì ptr `(1)` có `2` nghiệm phân biệt

    `=>\Delta > 0`

`<=>5^2-4(3m-1) > 0`

`<=>25-12m+4 > 0`

`<=>m < 29/12`

  `=>` Áp dụng Viét có: `{(x_1+x_2=-b/a=-5),(x_1.x_2=c/a=3m-1):}`

Ta có: `[x_1 ^2]/[x_2]-[x_2 ^2]/[x_1]+3=75/[x_1.x_2]`

`<=>[x_1 ^3-x_2 ^3]/[x_1.x_2]+[3x_1.x_2]/[x_1.x_2]=75/[x_1.x_2]`

  `=>(x_1-x_2)(x_1 ^2+x_1.x_2+x_2 ^2)+3x_1.x_2=75`

`<=>(x_1-x_2)[(x_1+x_2)^2-x_1.x_2]+3x_1.x_2=75`

`<=>(x_1-x_2)[(-5)^2-3m+1]+3(3m-1)=75`

`<=>(x_1-x_2)(26-3m)=78-9m`

`<=>x_1-x_2=[3(26-3m)]/[26-3m]`

`<=>x_1-x_2=3`

  Kết hợp với `x_1+x_2=-5`

Giải hệ  `=>{(x_1=-1),(x_2=-4):}`

Thay vào `x_1.x_2=3m-1` có:

    `-1.(-4)=3m-1`

`<=>m=5/3` (t/m)

=>x=m+1-my và m(m+1-my)+y=3m-1

=>x=m+1-my và m^2+m-m^2y+y=3m-1

=>y(-m^2+1)=3m-1-m^2-m=-m^2+2m-1 và x=m+1-my

=>y(m-1)(m+1)=(m-1)^2 và x=m+1-my

TH1: m=1

=>Hệ có vô số nghiệm

TH2: m=-1

=>Hệ vô nghiệm

TH3: m<>1; m<>-1

=>\(\left\{{}\begin{matrix}y=\dfrac{m-1}{m+1}\\x=m+1-\dfrac{m^2-m}{m+1}=\dfrac{m^2+2m+1-m^2+m}{m+1}=\dfrac{3m+1}{m+1}\end{matrix}\right.\)

\(P=x\cdot y=\dfrac{3m^2+m-3m-1}{\left(m+1\right)^2}=\dfrac{3m^2-2m-1}{m^2+2m+1}\)

\(=\dfrac{3m^2+6m+3-8m-4}{m^2+2m+1}=3-\dfrac{8m+4}{\left(m+1\right)^2}\)

Để P nhỏ nhất thì -(8m+4)/(m+1)^2 nhỏ nhất

=>8m+4=0

=>m=-1/2

(1): x+y=4

=>y=4-x

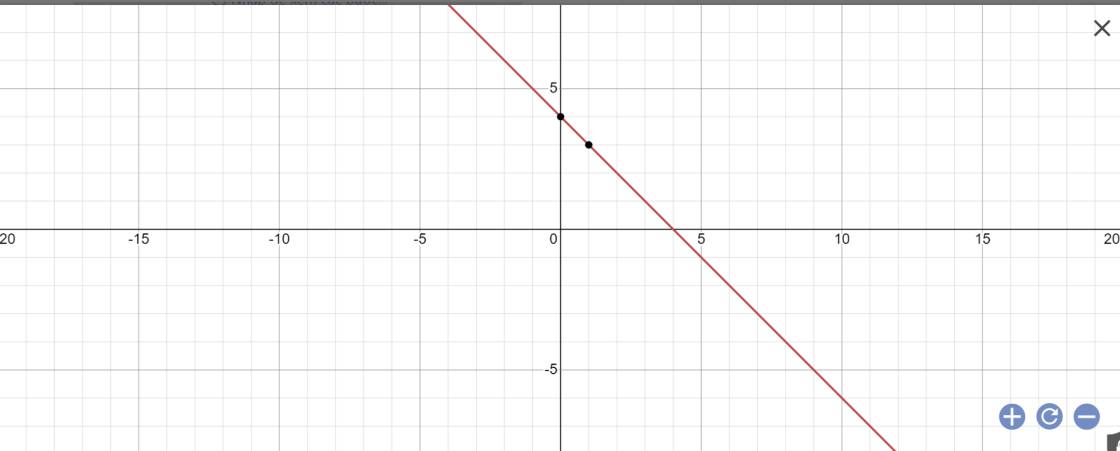
(2): 2x-y=-1

=>y=2x+1

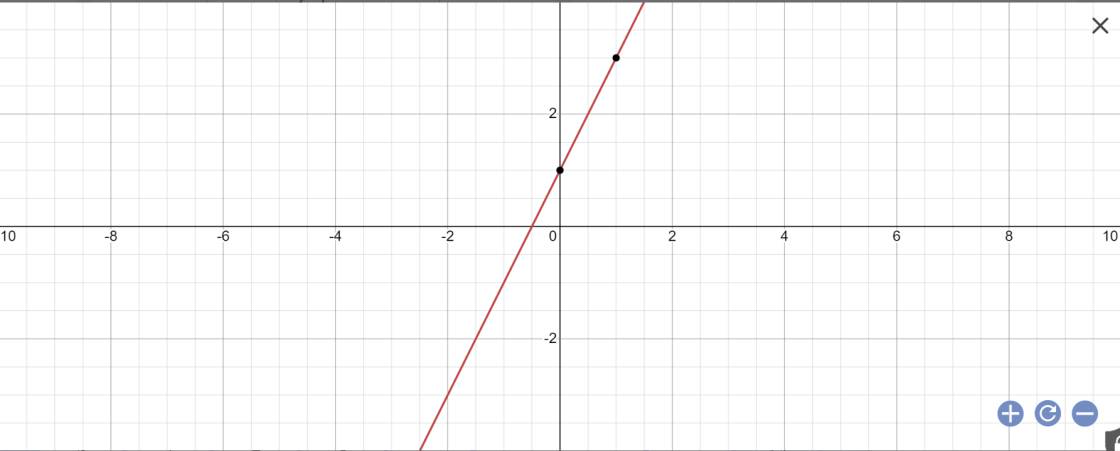
Bài 3:

\(\left\{{}\begin{matrix}x+y=3\\-mx-y=2m\end{matrix}\right.\left(1\right)\)

Ta có :

\(\left\{{}\begin{matrix}D=-1+m\\D_x=-3m-2m=-5m\\D_y=2m+3m=5m\end{matrix}\right.\)

Để (1) vô nghiệm \(\Leftrightarrow\left\{{}\begin{matrix}-1+m=0\\-5m\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m=1\\m\ne0\end{matrix}\right.\) \(\Leftrightarrow m=1\)

b) Để (1) có nghiệm duy nhất \(\Leftrightarrow-1+m\ne0\Leftrightarrow m\ne1\)

c) Để (1) có vô số nghiệm \(\Leftrightarrow\left\{{}\begin{matrix}-1+m=0\\-5m=0\\5m=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m=1\\m=0\\m=0\end{matrix}\right.\) \(\Leftrightarrow m\in\varnothing\)

a: Để hệ vô nghiệm thì \(\dfrac{1}{-m}=\dfrac{1}{-1}< >\dfrac{3}{2m}\)

=>m=1

b: Để hệ có nghiệm duy nhất thì 1/-m<>1/-1=-1

=>m<>1

c: Để hệ có vô số nghiệm thì \(\dfrac{1}{-m}=\dfrac{1}{-1}=\dfrac{3}{2m}\)

=>m=1 và 2m=-3

=>\(m\in\varnothing\)

Do \(2a-b=8\)

\(\Rightarrow b=2a-8\)

Ta có :

\(b=52,63\%\left(a+b\right)\)

\(\Leftrightarrow2a-8=52,63\%\left(a+2a-8\right)\)

\(\Leftrightarrow2a-8=0,5263\times a+2a\times0,5263-8\times0,5263\)

\(\Leftrightarrow2a-8=0,5263a+1,0526a-4,2104\)

\(\Leftrightarrow2a-0,5263a-1,0526a=8-4,2104\)

\(\Leftrightarrow0,4211a=3,7896\)

\(\Leftrightarrow a=8,999\approx9\)

\(\Rightarrow b=9,999\approx10\)

Ta lấy pt thứ 2 cộng 2 lần với pt thứ nhất ta được:

\(x^2+2xy+y^2+4x-4y+4=0\)

Hay: \(\left(x-y+2\right)^2=0\)

Ta suy ra \(y=x+2\). Thay trở lại pt thứ nhất của hệ ta được:

\(x^2-2x\left(x+2\right)+x-2\left(x+2\right)+3=0\)

Trương đương với: \(x^2+5x+1=0\)

Vì vậy có nghiệm: \(x=\frac{-5\pm\sqrt{21}}{2}\).

Do đó: \(y=x+2=\frac{-1\pm\sqrt{21}}{2}\)

Vậy hệ pt đã cho có 2 nghiệm \(\left(x,y\right)=\left(\frac{-5+\sqrt{21}}{2};\frac{-1+\sqrt{21}}{2}\right);\left(\frac{-5-\sqrt{21}}{2};\frac{-1-\sqrt{21}}{2}\right)\)

xy = 320 <=> y = 320/x

(x-16)(y+10)=320 <=> (x-16)((320/x)+10)=320 <=> 320+10x-160-(5120/x)=320 <=> 10x - (5120/x)=160 <=> 10x^2 - 160x-5120=160

=> x1=32 =>y1=10

x2=-16 =>y2=-20

\(A=4\sqrt{7}-3-15=4\sqrt{7}-18\\ B=\left(2\sqrt{3}+3\sqrt{3}-12\sqrt{3}\right):\sqrt{3}=-7\sqrt{3}:\sqrt{3}=-7\\ C=\sqrt{5}-\sqrt{3}-\sqrt{5}+1+\sqrt{3}=1\\ D=\left[\dfrac{\sqrt{5}\left(\sqrt{3}-2\right)}{2-\sqrt{3}}+\dfrac{\sqrt{7}\left(\sqrt{3}-1\right)}{1-\sqrt{3}}\right]\left(\sqrt{7}-\sqrt{5}\right)=\left(-\sqrt{7}-\sqrt{5}\right)\left(\sqrt{7}-\sqrt{5}\right)=-\left(7-5\right)=-2\\ E=\dfrac{\sqrt{3}\left(\sqrt{3}+2\right)}{\sqrt{3}}+\dfrac{\sqrt{2}\left(\sqrt{2}+1\right)}{\sqrt{2}+1}-\dfrac{\sqrt{3}-1}{1-\sqrt{3}}=\sqrt{3}+\sqrt{2}+1\\ F=\dfrac{\sqrt{5}\left(\sqrt{5}-2\right)}{\sqrt{5}}-\dfrac{2\left(\sqrt{5}+2\right)}{1}+\sqrt{\left(2-\sqrt{5}\right)^2}=\sqrt{5}-2-2\sqrt{5}-4+2-\sqrt{5}=-4-2\sqrt{5}\)