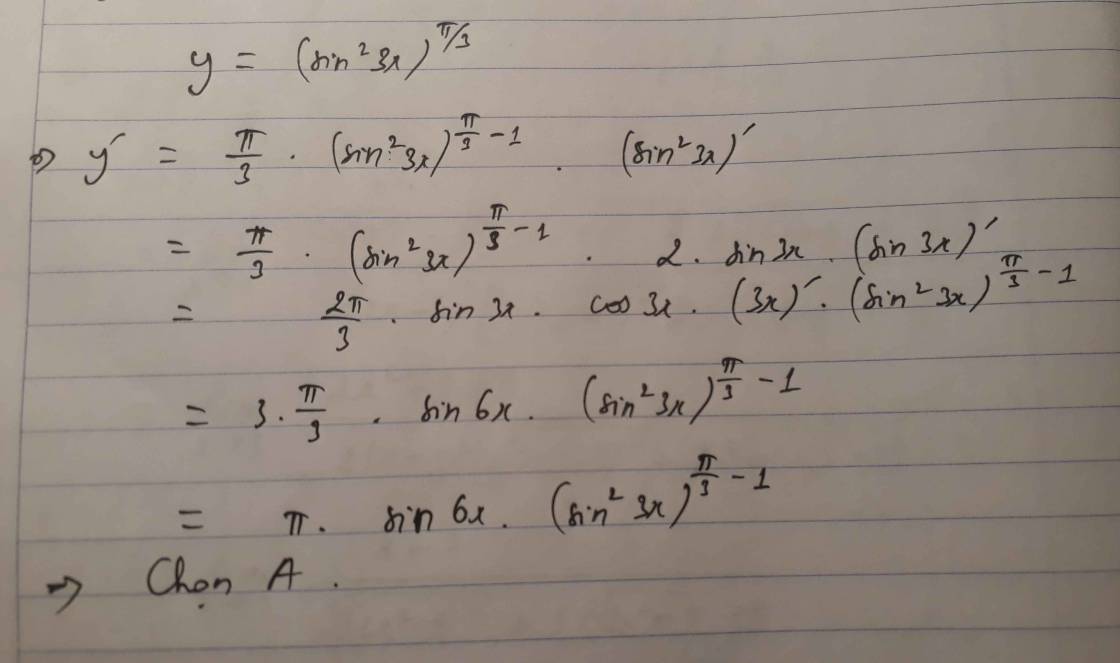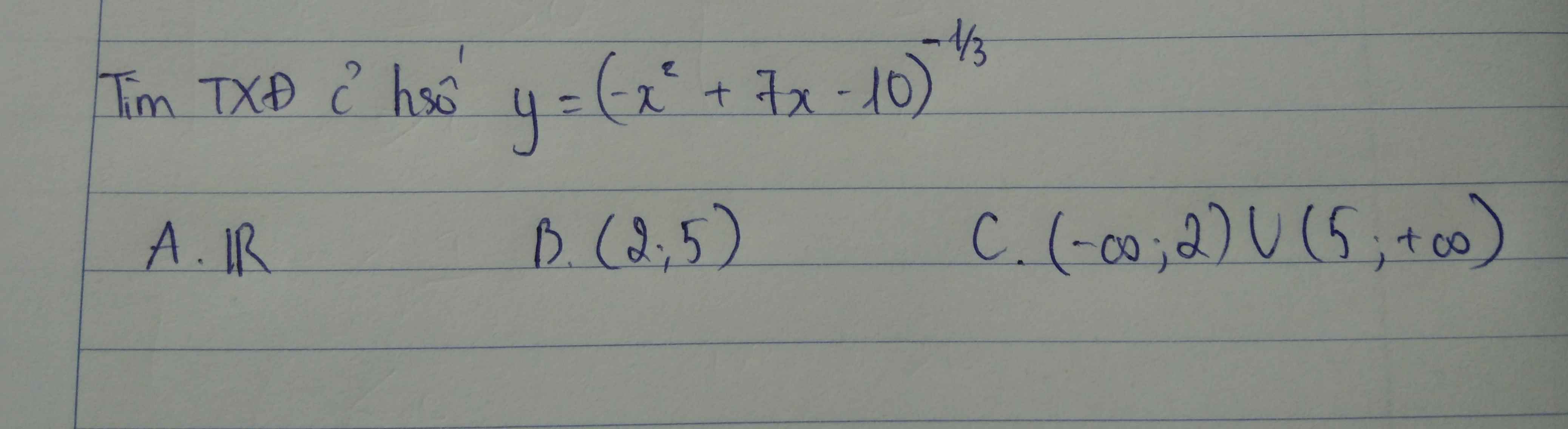Đạo hàm của hàm số $y = (sin^23x)^\frac{\pi}{3}$ là:
A. $y' = sin6x . \pi . (sin^23x)^{\frac{\pi}{3}-1}$
B. $y' = 2sin3x . \pi . (sin^23x)^{\frac{\pi}{3}-1}$
C. $y' = 3cos6x . \pi . (sin^23x)^{\frac{\pi}{3}-1}$
D. $y' = cos2x . \pi . (sin^23x)^{\frac{\pi}{3}-1}$