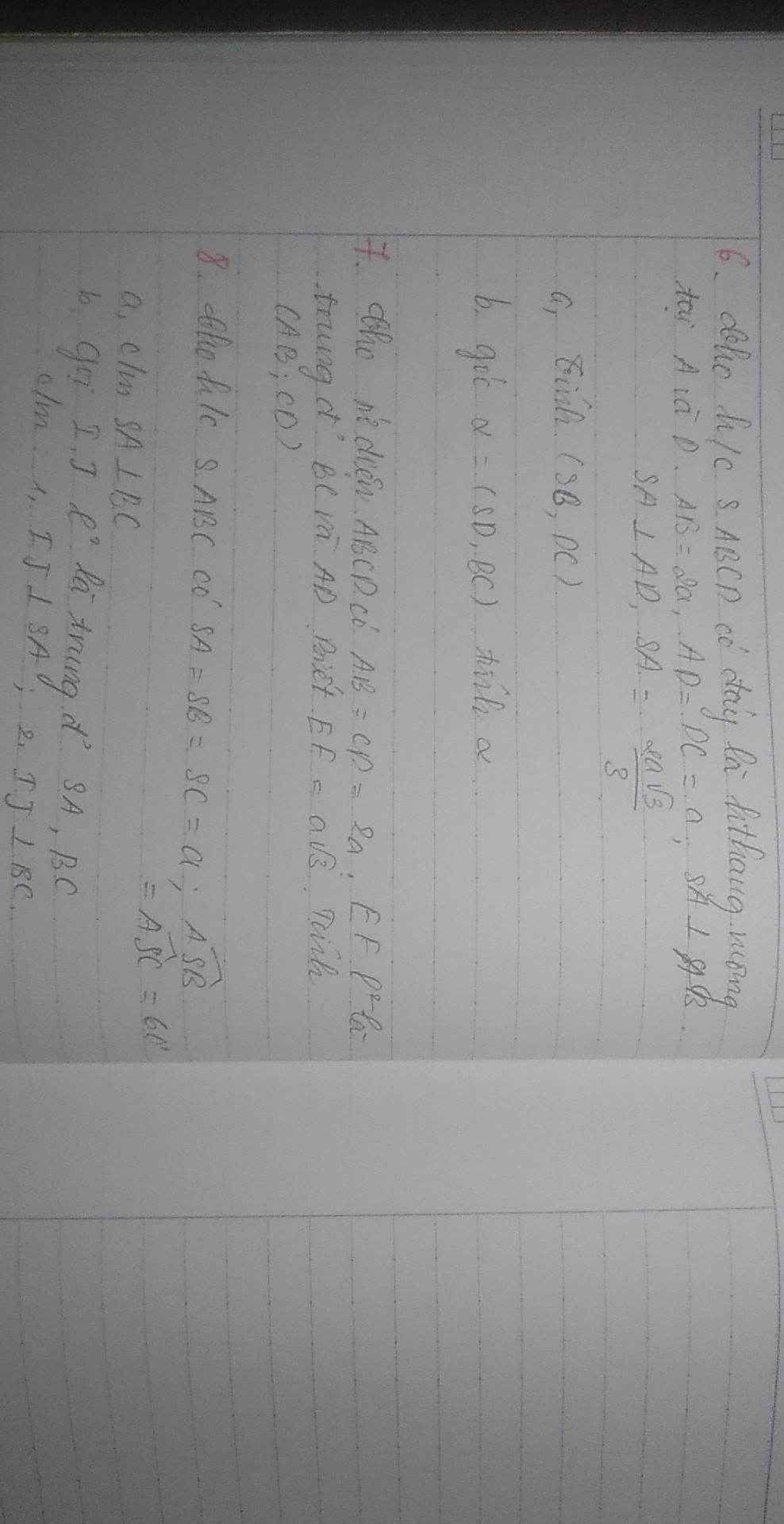Bài 2: Hai đường thẳng vuông góc

1: CB vuông góc AB

SA vuông góc BC

=>BC vuông góc (SAB)

=>BC vuông góc SB

=>ΔSBC vuông tại B

b: BC vuông góc AH

SB vuông góc AH

=>AH vuông góc (SBC)

=>AH vuông góc HK

=>ΔAHK vuông tại H

bạn ơi bạn làm đc phần nào rồi ? 

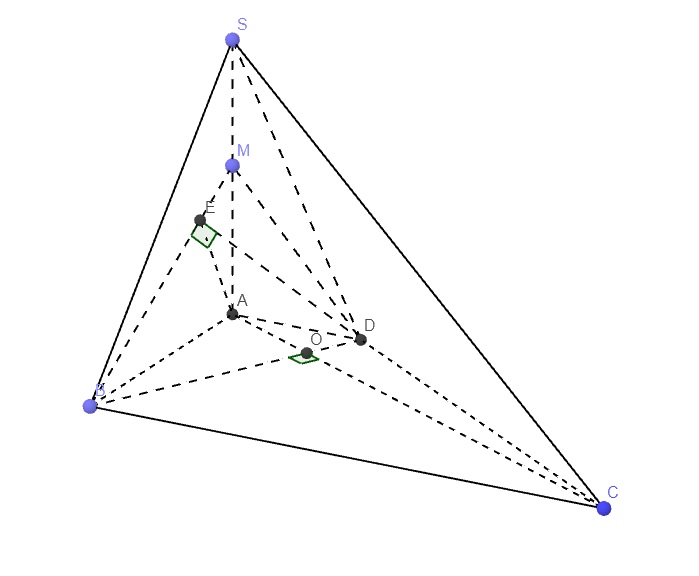
7:

Gọi M la trung điểm của AC

Xét ΔADC co AF/AD=AM/AC

nên FM//DC và FM=1/2DC=a

Xét ΔCAB co CM/CA=CE/CB

nên EM//AB và EM=1/2AB=a

\(cos\left(AB;CD\right)=\left|cos\left(\overrightarrow{AB};\overrightarrow{CD}\right)\right|=\left|cos\left(\overrightarrow{ME};\overrightarrow{MF}\right)\right|\)

\(=\left|cosFME\right|\)

\(=\left|\dfrac{MF^2+ME^2-FE^2}{2\cdot MF\cdot ME}\right|=\left|\dfrac{a^2+a^2-3a^2}{2\cdot a\cdot a}\right|=\dfrac{1}{2}\)

=>cos(AB;CD)=60 độ

a.

\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\BC\perp AB\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp SB\)

\(\Rightarrow\Delta SBC\) vuông tại B

b. \(\left\{{}\begin{matrix}SA\perp BD\\BD\perp SC\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\Rightarrow BD\perp AC\)

\(\Rightarrow\widehat{BCA}=\widehat{ABD}\) (góc có cạnh tương ứng vuông góc)

\(\Rightarrow AD=AB.tan\widehat{ABD}=AB.\dfrac{AB}{BC}=\dfrac{a}{2}\)

c. Theo c/m câu a ta có \(BC\perp\left(SAB\right)\), mà \(AD||BC\Rightarrow AD\perp\left(SAB\right)\)

\(\Rightarrow AD\perp BM\)

Mà \(BM\perp DE\) (do DE là đường cao ứng với BM)

\(\Rightarrow BM\perp\left(ADE\right)\Rightarrow BM\perp AE\)

Áp dụng hệ thức lượng trong tam giác vuông ABM:

\(AE=\dfrac{AM.AB}{\sqrt{AM^2+AB^2}}=\dfrac{ax}{\sqrt{a^2+x^2}}\)

Pitago tam giác vuông ADE:

\(DE^2=AE^2+AD^2=\dfrac{a^2x^2}{a^2+x^2}+\dfrac{a^2}{4}\)

Do \(AD=\dfrac{a}{2}\) không đổi nên DE max, min tương ứng khi AE max, min

Hiển nhiên \(AE\ge0\Rightarrow AE_{min}=0\) khi \(x=0\) khi đó DE min

\(AE^2=\dfrac{a^2x^2}{a^2+x^2}\le\dfrac{a^2x^2}{2ax}=\dfrac{ax}{2}\le\dfrac{a^2}{2}\)

\(\Rightarrow AE_{max}\) khi \(x=3\)

Đặt \(\overrightarrow{C'N}=x.\overrightarrow{C'D'}\)

\(\overrightarrow{AM}=\overrightarrow{AD}+\overrightarrow{DM}=\overrightarrow{AD}+\dfrac{1}{3}\overrightarrow{DC}=\overrightarrow{A'D'}+\dfrac{1}{3}\overrightarrow{D'C'}\)

\(\overrightarrow{B'N}=\overrightarrow{B'C'}+\overrightarrow{C'N}=\overrightarrow{A'D'}+x.\overrightarrow{C'D'}\)

\(AM\perp B'N\Rightarrow\overrightarrow{AM}.\overrightarrow{B'N}=0\)

\(\Rightarrow\left(\overrightarrow{A'D'}-\dfrac{1}{3}\overrightarrow{C'D'}\right)\left(\overrightarrow{A'D'}+x.\overrightarrow{C'D'}\right)=0\)

\(\Leftrightarrow A'D'^2-\dfrac{1}{3}x.C'D'^2=0\) (do \(A'D'\perp C'D'\Rightarrow\overrightarrow{A'D'}.\overrightarrow{C'D'}=0\))

\(\Rightarrow4-\dfrac{4}{3}x=0\Rightarrow x=3\)

Vậy N là điểm trên C'D' thỏa mãn \(\overrightarrow{C'N}=3\overrightarrow{C'D'}\)

a: Xét ΔAMB và ΔAMC có

AB=AC

AM chung

MB=MC

Do đó: ΔAMB=ΔAMC

b: Ta có: ΔABC cân tại A

mà AM là đường trung tuyến

nen AM là đường cao

=>a//BC

Gọi 2 góc kề bù lần lượt là\(\widehat{A}\) và \(\widehat{B}\)
Ta có: \(\widehat{A}+\widehat{B}=180^0\)

⇔\(\dfrac{1}{2}\widehat{A}+\dfrac{1}{2}\widehat{B}=\dfrac{1}{2}\left(\widehat{A}+\widehat{B}\right)=90^0\)

Vậy hai tia phân giác của hai góc kề bù thì vuông góc với nhau.