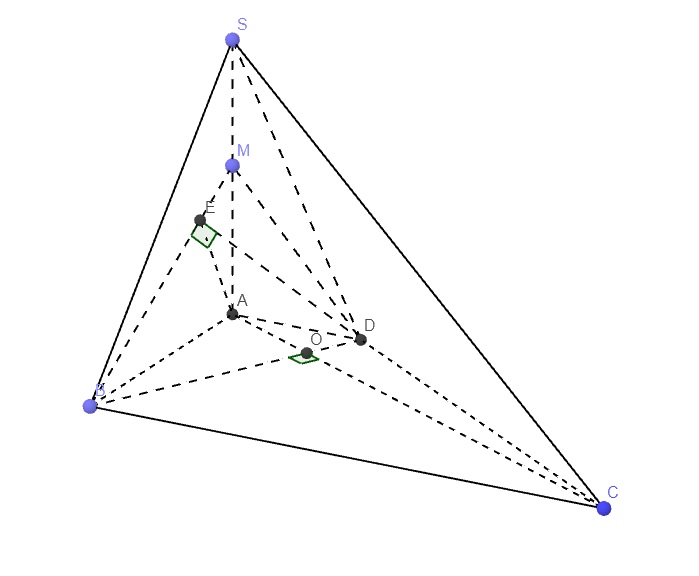
Cho hình chóp S. ABCD có SA vuông góc vs đáy và SA=a , đáy ABCD là hình thang vuông đường cao AB=a , BC=2a . Ngoài ra SC vuông góc BD . a ) Chứng minh ΔSBC vuông
b ) Tính theo a độ dài AD
c ) Gọi M là 1 điểm trên đoạn SA , đặt AM=x , vs 0≤x≤a . Tính độ dài đg cao DE của ΔBDM theo a và x . Xác định x để DE lớn nhất , nhỏ nhất
a.
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\BC\perp AB\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp SB\)
\(\Rightarrow\Delta SBC\) vuông tại B
b. \(\left\{{}\begin{matrix}SA\perp BD\\BD\perp SC\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\Rightarrow BD\perp AC\)
\(\Rightarrow\widehat{BCA}=\widehat{ABD}\) (góc có cạnh tương ứng vuông góc)
\(\Rightarrow AD=AB.tan\widehat{ABD}=AB.\dfrac{AB}{BC}=\dfrac{a}{2}\)
c. Theo c/m câu a ta có \(BC\perp\left(SAB\right)\), mà \(AD||BC\Rightarrow AD\perp\left(SAB\right)\)
\(\Rightarrow AD\perp BM\)
Mà \(BM\perp DE\) (do DE là đường cao ứng với BM)
\(\Rightarrow BM\perp\left(ADE\right)\Rightarrow BM\perp AE\)
Áp dụng hệ thức lượng trong tam giác vuông ABM:
\(AE=\dfrac{AM.AB}{\sqrt{AM^2+AB^2}}=\dfrac{ax}{\sqrt{a^2+x^2}}\)
Pitago tam giác vuông ADE:
\(DE^2=AE^2+AD^2=\dfrac{a^2x^2}{a^2+x^2}+\dfrac{a^2}{4}\)
Do \(AD=\dfrac{a}{2}\) không đổi nên DE max, min tương ứng khi AE max, min
Hiển nhiên \(AE\ge0\Rightarrow AE_{min}=0\) khi \(x=0\) khi đó DE min
\(AE^2=\dfrac{a^2x^2}{a^2+x^2}\le\dfrac{a^2x^2}{2ax}=\dfrac{ax}{2}\le\dfrac{a^2}{2}\)
\(\Rightarrow AE_{max}\) khi \(x=3\)