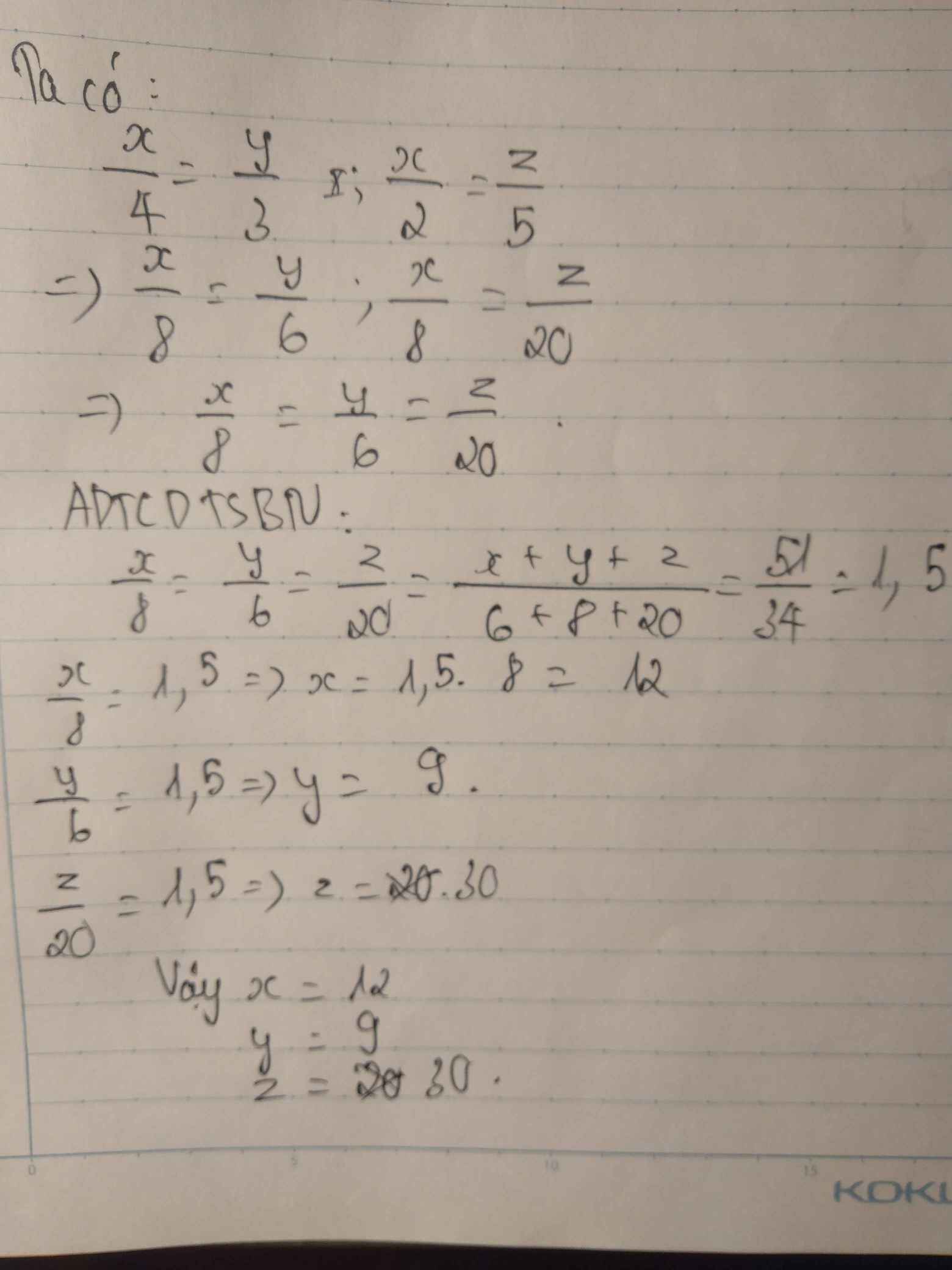Tìm x,y,z?
Có \(\dfrac{x}{4}=\dfrac{y}{3}\)
\(\dfrac{z}{5}=\dfrac{x}{2}\Leftrightarrow\dfrac{z}{10}=\dfrac{x}{4}\)
\(\Rightarrow\dfrac{x}{4}=\dfrac{y}{3}=\dfrac{z}{10}\)
Áp dụng TCDTSBN có:
\(\dfrac{x}{4}=\dfrac{y}{3}=\dfrac{z}{10}=\dfrac{x+y+z}{4+3+10}=\dfrac{51}{17}=3\)
Do đó \(\dfrac{x}{4}=3;\dfrac{y}{3}=3;\dfrac{z}{10}=3\)
\(\Rightarrow x=12;y=9;z=30\)
Ta có: \(\dfrac{x}{4}=\dfrac{y}{3}\)
mà \(\dfrac{x}{4}=\dfrac{z}{10}\left(\dfrac{x}{2}=\dfrac{z}{5}\right)\)
nên \(\dfrac{x}{4}=\dfrac{y}{3}=\dfrac{z}{10}\)
mà x+y+z=51
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{4}=\dfrac{y}{3}=\dfrac{z}{10}=\dfrac{x+y+z}{4+3+10}=\dfrac{51}{17}=3\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{x}{4}=3\\\dfrac{y}{3}=3\\\dfrac{z}{10}=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=12\\y=9\\z=30\end{matrix}\right.\)
Vậy: (x,y,z)=(12;9;30)
đặt:
x/2=z/5>x/4=z/10
ta được
x/4=y/3=z/10 [x+y+z=51]
áp dụng tính chất dẫy tỉ số bằng nhau.ta có
x/4=y/3=z/10=x/4+y/3+z/10=51/17=3
do đó:
x/4=3 y/3=3 z/10=3
x=12 y=9 z=30
vậy x=12,y=9,z=30