Với x>4
\(PT\Leftrightarrow1!+2!+...+x!=y^2\)
\(\Leftrightarrow1!+2!+3!+4!+...+x!=y^2\)
\(\Leftrightarrow33+5!+...+x!=y^2\)
Mà x>4\(\Rightarrow5!+...+x!⋮10\)
\(\Rightarrow y^2\) có chữ số tận cùng là 3(vô lí)
Vậy thử các TH x<=4
Tìm nghiệm nguyên dương của phương trình : \(\sqrt{x+2\sqrt{3}}=\sqrt{y}+\sqrt{z}\)
Tìm nghiệm nguyên dương của phương trình : 2xyz=x+y+z
1, tìm nghiệm nguyên dương của phương trình 3xy+6x+y-52=0
1) Chứng minh rằng: \(x^3-7y=51\) không có nghiệm nguyên
2) Tìm nghiệm nguyên của phương trình \(x^2-5y^2=27\)
3) Tìm nghiệm nguyên dương
a) \(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=1\)
b)\(\dfrac{1}{x}+\dfrac{1}{y}=z\)
Tìm nghiệm nguyên không âm thỏa mãn phương trình: x^2=y^2 + căn y+1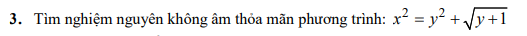
Tìm nghiệm nguyên của phương trình: \(x^2-25=y.\left(y+6\right)\)
Tìm nghiệm nguyên ko âm của phương trình: x²=y²+y+1
1. Tìm nghiệm nguyên của phương trình xy-x+y=4
ho phương trình : x^2 - (m+1)x + m = 0
Tìm m để phương trình có hai nghiệm trái dấu và nghiệm dương có giá trị tuyệt đối lớn hơn
Giải phương trình nghiệm nguyên \(x^2+y^2+2x+2y=x^2y^2-1\)
