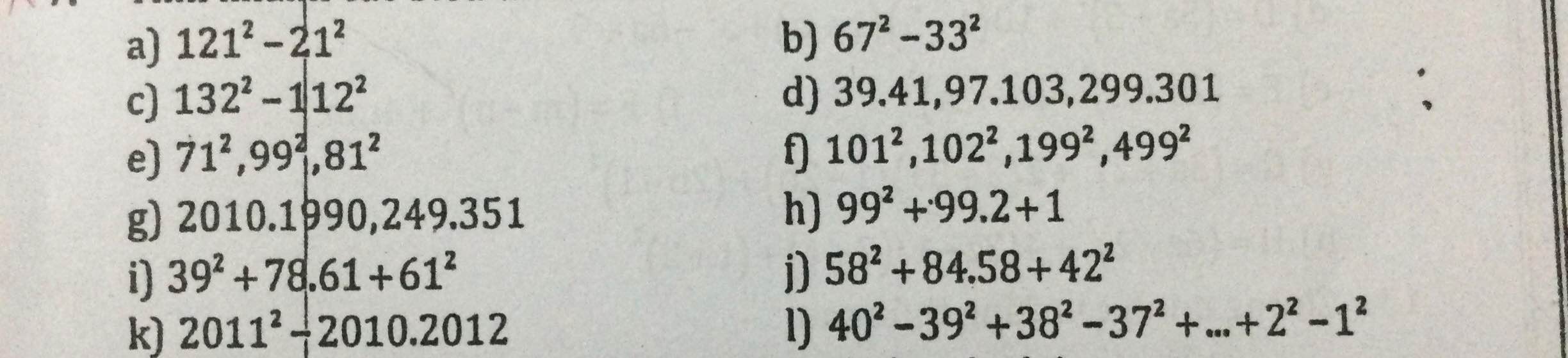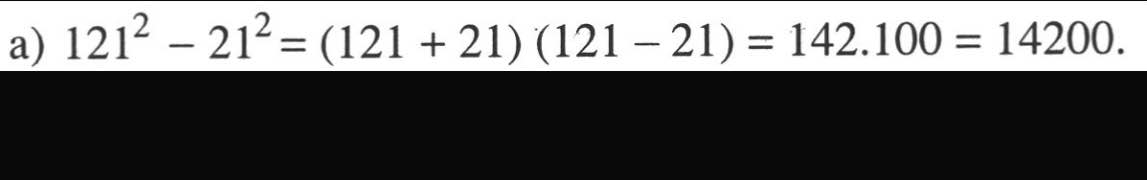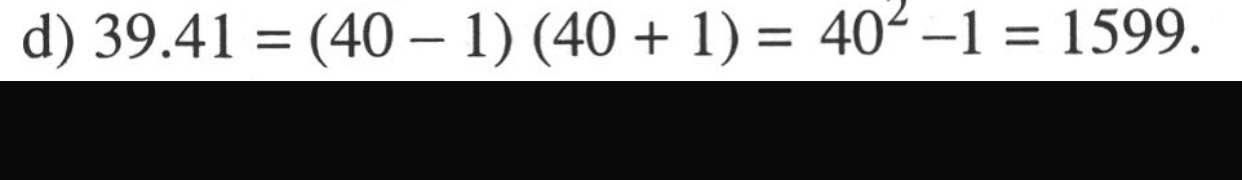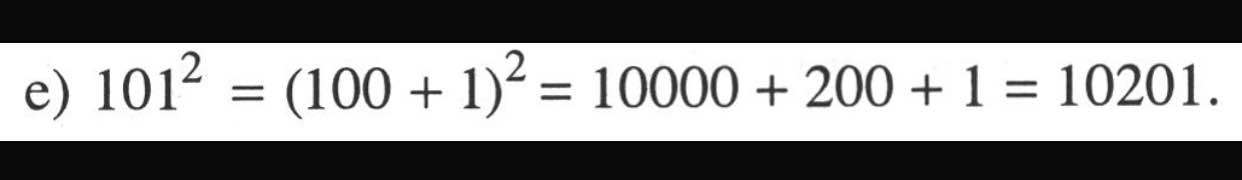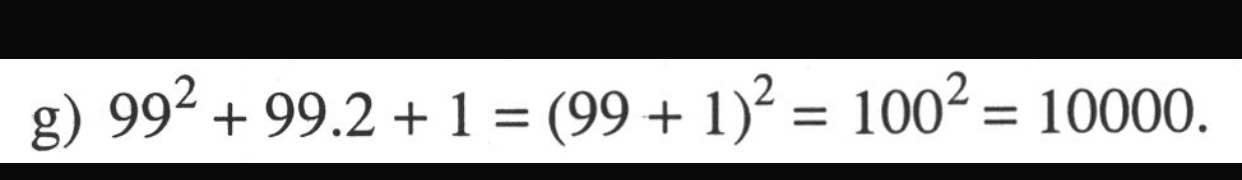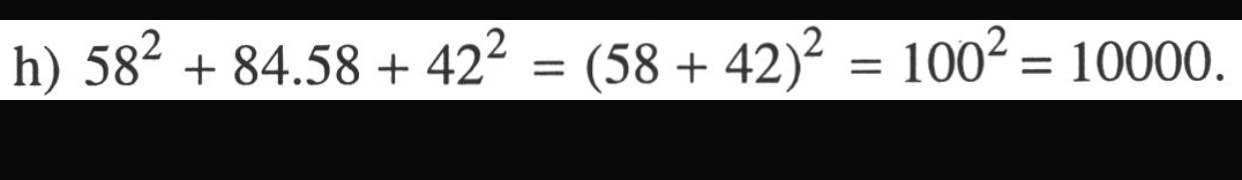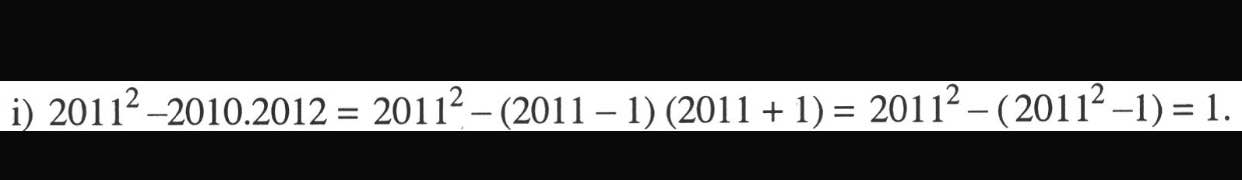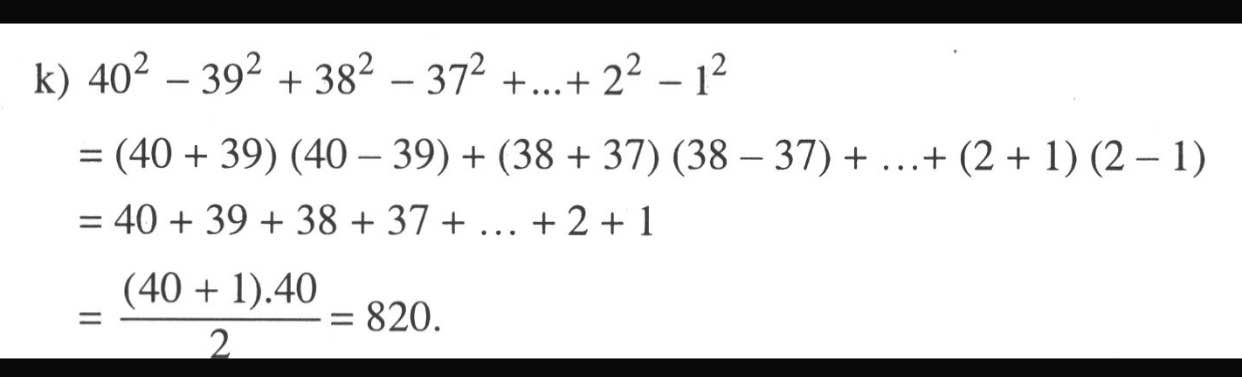l) Ta có: \(40^2-39^2+38^2-37^2+...+2^2-1^2\)
\(=40+39+38+37+...+2+1\)
\(=41\cdot20=820\)
h) Ta có: \(99^2+2\cdot99+1\)
\(=\left(99+1\right)^2\)
=10000
k) Ta có: \(2011^2-2010\cdot2012\)
\(=2011^2-2011^2+1\)
=1
i) Ta có: \(39^2+78\cdot61+61^2\)
\(=39^2+2\cdot39\cdot61+61^2\)
\(=\left(39+61\right)^2\)
=10000