ĐKXĐ: ...
\(4x^2-4x-8=\sqrt{2x+6}-2\)
\(\Leftrightarrow\left(x+1\right)\left(4x-8\right)=\dfrac{2\left(x+1\right)}{\sqrt{2x+6}+2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\2x-4=\dfrac{1}{\sqrt{2x+6}+2}\left(1\right)\end{matrix}\right.\)
Xét (1), đặt \(\sqrt{2x+6}=t\ge0\Rightarrow2x=t^2-6\)
\(\Rightarrow t^2-10=\dfrac{1}{t+2}\)
\(\Leftrightarrow t^3+2t^2-10t-21=0\)
\(\Leftrightarrow\left(t+3\right)\left(t^2-t-7\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}t=-3< 0\left(loại\right)\\t=\dfrac{1-\sqrt{29}}{2}< 0\left(loại\right)\\t=\dfrac{1+\sqrt{29}}{2}\end{matrix}\right.\)
\(\Rightarrow\sqrt{2x+6}=\dfrac{1+\sqrt{29}}{2}\)
\(\Rightarrow x=\dfrac{3+\sqrt{29}}{4}\)
Cách khác:
ĐKXĐ: \(x\ge-3\).
Đặt \(\sqrt{2x+6}=a\left(a\ge0\right)\).
Phương trình đã cho tương đương:
\(4x^2-2x=a^2+a\)
\(\Leftrightarrow\left(2x-a\right)\left(2x+a\right)-\left(2x+a\right)=0\)
\(\Leftrightarrow\left(2x+a\right)\left(2x-a-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=-a\\2x=a+1\end{matrix}\right.\).
+) \(2x=-a\Leftrightarrow-2x=\sqrt{2x+6}\Leftrightarrow\left\{{}\begin{matrix}x\le0\\4x^2=2x+6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\le0\\4x^2-2x-6=0\end{matrix}\right.\Leftrightarrow x=-1\) (TMĐK).
+) \(2x=a+1\Leftrightarrow2x-1=\sqrt{2x+6}\Leftrightarrow\left\{{}\begin{matrix}x\ge\dfrac{1}{2}\\\left(2x-1\right)^2=2x+6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ge\dfrac{1}{2}\\4x^2-6x-5=0\end{matrix}\right.\Leftrightarrow x=\dfrac{\sqrt{29}+3}{4}\)(TMĐK).
Vậy...

 Hộ em ạ Cảm ơn
Hộ em ạ Cảm ơn 




 Gải chi tiết hộ em ạ Cảm ơn !
Gải chi tiết hộ em ạ Cảm ơn !


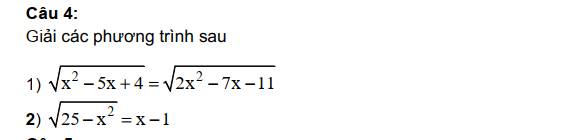







 Giải chi tiết hộ em với ạ
Giải chi tiết hộ em với ạ