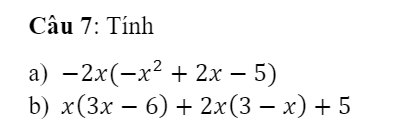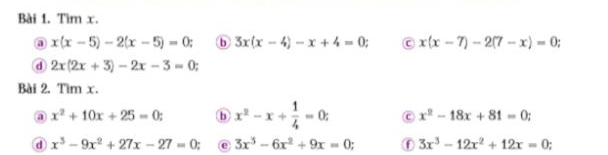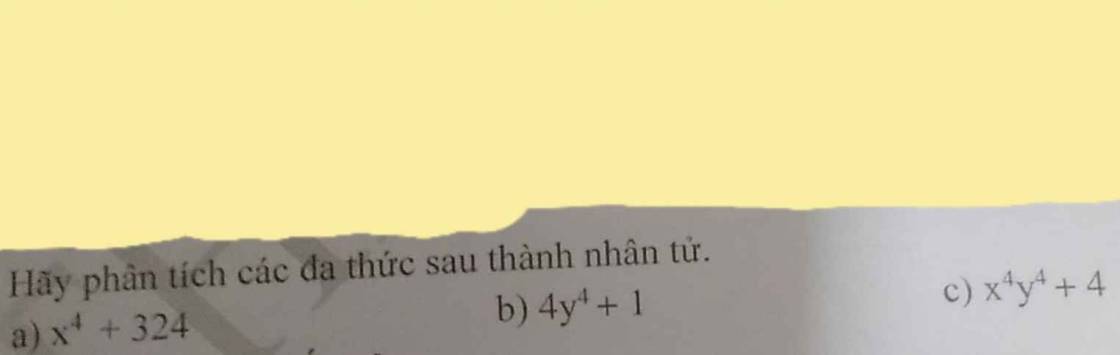Question

Giúp vs ạ

Answer 1

1) Giải:

a) \(\left(x+2\right)^2-2\left(x+2\right)\left(x-8\right)+\left(x-8\right)^2\)

= \(\left(x+2-x+8\right)^2=10^2=100\)

Vậy biểu thức trên không phụ thuộc vào biến.

b) \(\left(x+y-z-t\right)^2-\left(z+t-x-y\right)^2\)

= \(\left(x+y-z-t-z-t+x+y\right)\left(x+y-z-t+z+t-x-y\right)\)

= \(\left(2x+2y-2z-2t\right).0=0\)

Vậy biểu thức trên không phụ thuộc vào biến.

2) Giải:

Ta có: \(n^3-n=n\left(n^2-1\right)=n.\left(n-1\right).\left(n+1\right)\)

Tích của 3 số nguyên liên tiếp sẽ chia hết cho 6.

Mà n-1 ; n và n+1 là ba số nguyên liên tiếp ( n \(\in\) Z )

Nên n(n-1)(n+1) chia hết cho 6 hay n³-n chia hết cho 6.

3) Giải:

Ta có: \(x+3y=xy+3\)

\(\Leftrightarrow x+3y-xy-3=0\)

\(\Leftrightarrow-x\left(y-1\right)+3\left(y-1\right)=0\)

\(\Leftrightarrow\left(y-1\right)\left(3-x\right)=0\)

\(\Leftrightarrow\left\{{}\begin{matrix}y-1=0\\3-x=0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}y=1\\x=3\end{matrix}\right.\)

Vậy ( x ; y ) = ( 3 : 1 )

Answer 2

Câu 1:

\(\text{ a) }\left(x+2\right)^2-2\left(x+2\right)\left(x-8\right)+\left(x-8\right)^2\\ =\left[\left(x+2\right)-\left(x-8\right)\right]^2\\ =\left(x+2-x+8\right)^2\\ =10^2=100\\ \text{Vậy giá trị của biểu thức không phụ thuộc vào biến.}\\ \)

\(\text{b) }\left(x+y-z-t\right)^2-\left(z+t-x-y\right)^2\\ =\left[\left(x+y-z-t\right)+\left(z+t-x-y\right)\right]\left[\left(x+y-z-t\right)-\left(z+t-x-y\right)\right]\\ =\left(x+y-z-t+z+t-x-y\right)\left(x+y-z-t-z-t+x+y\right)\\ =\left[\left(x-x\right)+\left(y-y\right)-\left(z-z\right)-\left(t-t\right)\right]\left(x+y-z-t-z-t+x+y\right)\\ =0\cdot\left(x+y-z-t-z-t+x+y\right)\\ =0\\ \text{Vậy giá trị của biểu thức không phụ thuộc vào biến.}\)

Answer 3

Câu 2 : \(\dfrac{\text{Giải.}}{ }\)

\(\text{Ta có : }n^3-n\\ =n\left(n^2-1\right)\\ =n\left(n-1\right)\left(n+1\right)\)

Vì \(n\left(n-1\right)\left(n+1\right)\) là 3 số tự nhiên liên tiếp.

nên \(\Rightarrow n\left(n-1\right)\left(n+1\right)⋮2;3\)

Mà \(2\) và \(3\) là 2 số nguyên tố cùng nhau.

\(\Rightarrow n\left(n-1\right)\left(n+1\right)⋮2\cdot3\)

\(\Rightarrow n\left(n-1\right)\left(n+1\right)⋮6\left(đpcm\right)\)

Vậy \(n^3-n⋮6\)

Answer 4

Câu 3:

\(x+3y=xy+3\\ \Leftrightarrow x+3y-\left(xy+3\right)=0\\\Leftrightarrow x+3y-xy-3=0\\ \Leftrightarrow\left(x-xy\right)+\left(3y-3\right)=0\\ \Leftrightarrow x\left(1-y\right)-\left(3-3y\right)=0\\ \Leftrightarrow x\left(1-y\right)-3\left(1-y\right)=0\\ \Leftrightarrow\left(x-3\right)\left(1-y\right)=0\\ \Leftrightarrow\left\{{}\begin{matrix}x-3=0\\1-y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=1\end{matrix}\right.\)

Vậy \(x=3;y=1\)