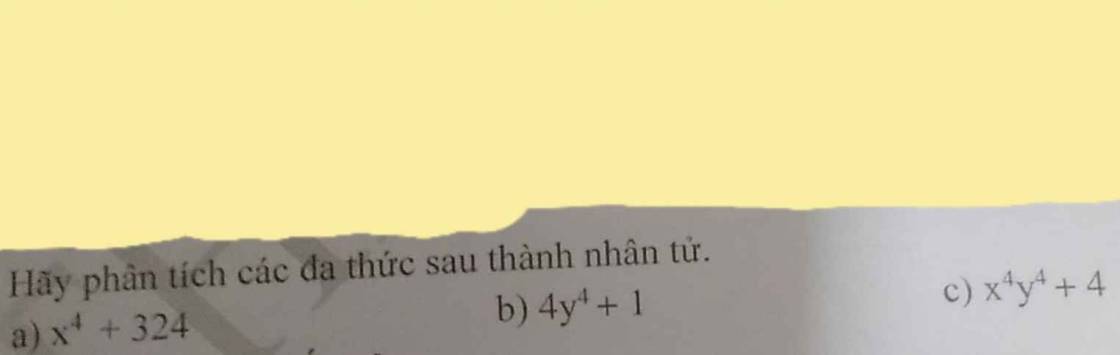a: \(x^4+324\)
\(=x^4+36x^2+324-36x^2\)
\(=\left(x^2\right)^2+2\cdot x^2\cdot18+18^2-36x^2\)
\(=\left(x^2+18\right)^2-36x^2\)
\(=\left(x^2-6x+18\right)\left(x^2+6x+18\right)\)
b: \(4y^4+1\)
\(=4y^4+4y^2+1-4y^2\)
\(=\left(2y^2+1\right)^2-\left(2y\right)^2\)
\(=\left(2y^2-2y+1\right)\left(2y^2+2y+1\right)\)
c: \(x^4y^4+4\)
\(=x^4y^4+4x^2y^2+4-4x^2y^2\)
\(=\left(x^2y^2+2\right)^2-\left(2xy\right)^2\)
\(=\left(x^2y^2+2-2xy\right)\left(x^2y^2+2+2xy\right)\)
\(a,x^4+324\\=[(x^2)^2+2\cdot x^2\cdot18+18^2]-2\cdot x^2\cdot18\\=(x^2+18)^2-36x^2\\=(x^2+18)^2-(6x)^2\\=(x^2+18-6x)(x^2+18+6x)\\b,4y^4+1\\=[(2y^2)^2+2\cdot2y^2\cdot1+1^2]-4y^2\\=(2y^2+1)^2-(2y)^2\\=(2y^2+1-2y)(2y^2+1+2y)\)
\(c,x^4y^4+4\\=[(x^2y^2)^2+2\cdot x^2y^2\cdot2+2^2]-4x^2y^2\\=(x^2y^2+2)^2-(2xy)^2\\=(x^2y^2+2-2xy)(x^2y^2+2+2xy)\\Toru\)