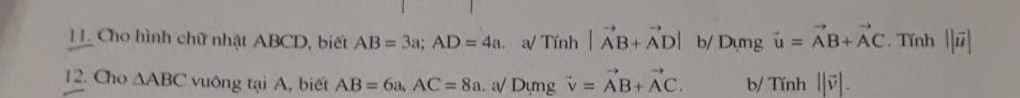11:

a: ABCD là hình chữ nhật
=>vecto AB+vecto AD=vecto AC
\(AC=\sqrt{\left(3a\right)^2+\left(4a\right)^2}=5a\)
\(\left|\overrightarrow{AB}+\overrightarrow{AD}\right|=\left|\overrightarrow{AC}\right|=AC=5a\)
b: Gọi M là trung điểm của BC
=>BM=MC=4a/2=2a
Trên tia đối của tia MA lấy D sao cho M là trung điểm của AD
Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
=>ABDC là hình bình hành
=>\(\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AD}=2\cdot\overrightarrow{AM}\)
\(AM=\sqrt{AB^2+BM^2}=\sqrt{\left(3a\right)^2+\left(2a\right)^2}=a\sqrt{13}\)
=>\(\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=2\cdot AM=2a\sqrt{13}\)