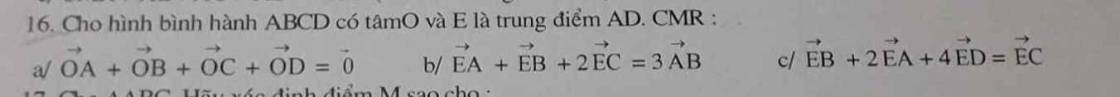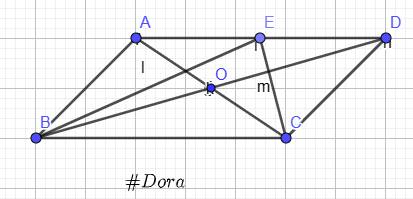
`a)` Vì `O` là trung điểm của `AC;BD`
`=>{(\vec{OA}=-\vec{OC}),(\vec{OB}=-\vec{OD}):}`
Ta có: `\vec{OA}+\vec{OB}+\vec{OC}+\vec{OD}`
`=-\vec{OC}-\vec{OD}+\vec{OC}+\vec{OD}=0`
`b)` Vì `E` là trung điểm `AD=>\vec{EA}=-\vec{ED}`
Ta có: `\vec{EA}+\vec{EB}+2\vec{EC}`
`=\vec{EA}+\vec{EA}+\vec{AB}+2\vec{ED}+2\vec{DC}`
`=-2\vec{ED}+\vec{AB}+2\vec{ED}+2\vec{AB}=3\vec{AB}`
`c)` Ta có: `\vec{EB}+2\vec{EA}+4\vec{ED}`
`=\vec{EB}-2\vec{ED}+4\vec{ED}`
`=\vec{EB}+2\vec{ED}`
`=\vec{EA}+\vec{AB}+2\vec{ED}`
`=-\vec{ED}+\vec{AB}+2\vec{ED}`
`=\vec{AB}+\vec{EC}+\vec{CD}` (Mà `\vec{AB}=-\vec{CD}`)
`=\vec{EC}`