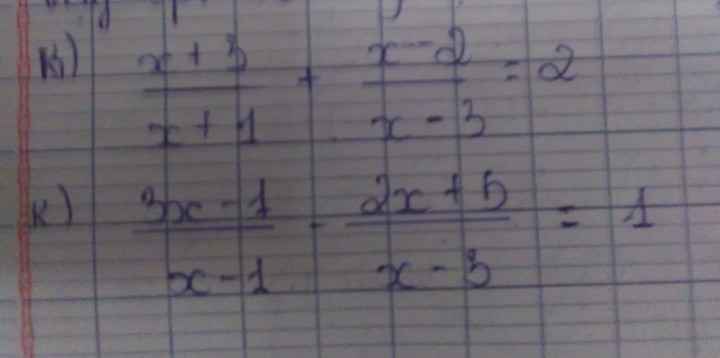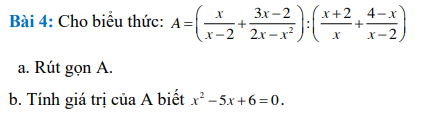CAU 4 NAO BN, ( BAI MAY? TRANG MAY?)
Ta có:
\(x^4+x^3+x^2+x+1=0\) ( 1 )
*Với x = 0 , phương trình (1) => 1 = 0 ( vô lý ).
Vậy 0 không phải là nghiệm của phương trình.
*Với \(x\ne0\), chia 2 vế phương trình cho \(x^2\), ta được:
\(x^2+x+1+\dfrac{1}{x}+\dfrac{1}{x^2}=0\)
\(\Rightarrow x^2+\dfrac{1}{x^2}+x+\dfrac{1}{x}+1=0\) ( 2 )
Đặt \(t=x+\dfrac{1}{x}\Rightarrow t^2=\left(x+\dfrac{1}{x}\right)^2\)
\(=x^2+x+\dfrac{1}{x^2}\)
\(\Rightarrow t^2-2=x^2+\dfrac{1}{x^2}\)
Khi đó phương trình (2) trở thành:
\(t^2-2+t+1=0\)
\(\Rightarrow t^2+t-1=0\)
\(\Rightarrow\left\{{}\begin{matrix}t=\dfrac{-1+\sqrt{5}}{2}\\t=\dfrac{-1-\sqrt{5}}{2}\end{matrix}\right.\) ( T bấm máy :)) Còn muốn tính xài denta nhé! )
*Với \(t=\dfrac{-1-\sqrt{5}}{2}\Rightarrow x+\dfrac{1}{x}=\dfrac{-1-\sqrt{5}}{2}\) ( vô nghiệm ).
\(t=\dfrac{-1+\sqrt{5}}{2}\Rightarrow x+\dfrac{1}{x}=\dfrac{-1-\sqrt{5}}{2}\) ( vô nghiệm ).
Vậy phương trình vô nghiệm.
cách khác câu b
ta thấy x = 1 không phải nghiệm của pt
=> x khác 1
Khi đó nhân cả 2 vế của pt đã cho với x - 1 ta được
x5 - 1 = 0 <=> x5 = 1 <=> x = 1, mâu thuẫn
Vậy ...
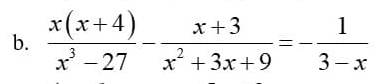giúp với ạ
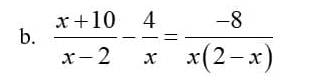giúp mình với ạ
