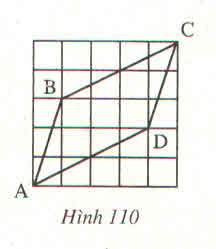
∆AHB và ∆ CKD có:
HB=KD.
AHB^=CKD^
AH=Ck
Nên ∆ AHB = ∆ CKD(c.g.c)
suy ra AB=CD.
tương tự ∆ CEB = ∆ AFD(c.g.c)
suy ra BC=AD.
b) ∆ABD và ∆CDB có:
AB=CD(câu a)
BC=AD(câu a)
BD chung.
Do đó ∆ABD=∆CDB(c.c .c)
Suy ra ˆABD=CDB^
Vậy AB // CD( hai góc so le trong bằng nhau)
Xét ∆AHB và ∆ CKD có:
HB=KD.
ˆAHB=ˆCKD
AH=CK
=> ∆ AHB = ∆ CKD(c.g.c)
=> AB=CD.( 2 canh tương ứng)
tương tự ∆ CEB = ∆ AFD(c.g.c)
=> BC=AD.
b) ∆ABD và ∆CDB có:
AB=CD(CMT)
BC=AD(CMT)
BD chung.
=> ∆ABD=∆CDB(c.c .c)
=> ˆABD^=ˆCDB( 2 góc tương ứng)
=> AB // CD( hai góc so le trong bằng nhau)
Xem thêm tại: http://loigiaihay.com/bai-45-trang-125-sach-giao-khoa-toan-7-tap-1-c42a5103.html#ixzz4nvM2UGda