Chúng ta đã biết đến định lý Pi-ta-go trong chương trình hình học lớp 7.
Định lý được phát biểu như sau:
Trong một tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
Định lý Pi-ta-go đóng một vai trò quan trọng trong lịch sử toán học bởi nó là cốt lõi của nhiều vấn đề trong hình học, là cầu nối giữa hình học và đại số và là nền tảng của lượng giác. Một lý do nữa khiến định lý Pi-ta-go nhận được nhiều tán thưởng chính là số lượng các chứng minh đóng góp cho nó. Có hơn 400 chứng minh được biết tới, trong đó có chứng minh của Einistein, một cô bé mù 12 tuổi và của Leonardo DaVinci.
Chứng minh sau đây, sử dụng cách chia nhỏ hình, được cho là của chính Pytago. Chứng minh xứng đáng được đánh giá cao bởi nó không cần một lời diễn giải nào và hết sức sơ cấp:

--- Câu hỏi dành cho các bạn ---
Hãy sưu tập các cách chứng minh của định lý Pi-ta-go và có thể phát minh ra cách chứng minh của chính mình.
Mỗi cách chứng minh đúng sẽ được 2GP.
Cách 1:
Chứng minh:
Xét các tam giác vuông như hình vẽ:
Ta có: \(S_{ADEF}=S_{BCPQ}+4.S_{ABC}\)
\(\Rightarrow\left(b+c\right)^2=a^2+4.\dfrac{bc}{2}\)
\(\Rightarrow b^2+2.bc+c^2=a^2+2.bc\)
Trừ cả hai vế cho 2.bc:
\(\Leftrightarrow b^2+c^2=a^2\) (đpcm)
Cách 1:Ghép hình.
Xếp các tam giác vuông như hình vẽ.
Chứng minh.
Đặt \(AB=a;AM=b;BM=c\)
Ta có:
\(S_{ABCD}=S_{MNPQ}+4.S_{AMB}\)
\(\Rightarrow a^2=\left(c-b\right)^2+4.\dfrac{bc}{2}\)
\(\Rightarrow a^2=c^2-2cb+b^2+2cb=c^2+b^2\)
\(\Rightarrow a^2=b^2+c^2\) hay \(AB^2=AM^2+BM^2\)(đpcm)
Nguồn: Chuyên đề “20 cách chứng minh định lý Py-Ta-go” - Giáo Án, Bài Giảng
Một số cách chứng minh định lí Pitago
Cách 1:
Dựng hình và kiểm tra
1. Vẽ một tam giác vuông và các hình vuông trên các cạnh của nó (dùng công cụ custom)
2. Kéo dài tia HA, lấy điểm A’ đối xứng với điểm H qua A bằng cách :
+ Chọn đoạn HA và điểm A
+ Chọn menu Transform --> Rotate --> degrees =180
3. Vẽ một đường thẳng đi qua điểm B và vuông góc với đoạn AA’, Vẽ điểm giao K của 2 đường này.
( Hình bên minh họa cho các bước từ 1 đến 3)
4. Vẽ hình vuông A’KLM.
(Sử dụng công cụ Custom tool như đã giới thiệu ở bài 1)
5. Vẽ Đoạn BK, GM, FL.
6. Làm ẩn đi đường BK.
7. Tô màu cho 4 mảnh trong hình vuông trên cạnh huyền.
8. Đánh dấu vectơ EJ và dịch chuyển 4 đỉnh và 4 cạnh của hình vuông BCDE theo vectơ này (để được hình vuông bên dưới hình vuông trên cạnh b có diện tích bằng diện tích hình vuông BCDE )
+ Đánh dấu theo thứ tự điểm E, J
+ Chọn menu Transform --> Mark vector
+ Đánh dấu 4 cạnh và 4 đỉnh của hình vuông BCDE
+ Chọn vào Menu Transform --> Translate.
9. Như vậy miền diện tích trên cạnh b bây giờ là a2 + b2 . Sử dụng công cụ Translator để di chuyển các các mảnh là bản sao của các mảnh trong hình
vuông trên cạnh huyền vào trong miền có diện tích a2 + b2 trên cạnh b.
Chú ý:
- Hãy thử thay đổi tam giác của bạn, và quan sát xem các mảnh tương ứng còn lại có bằng nhau nữa không.?
- Chú ý rằng, trong trương hợp dựng hình như thế này cạnh b cần phải luôn được giữ là cạnh bên dài hơn nếu không thì sự dựng hình như trên sẽ bị sai.
- Trường hợp đặc biệt trước khi việc dựng hình bi sai là trương hợp cạnh b dài bằng cạnh a thì hình vuông A’KLM biến mất.
- Bạn hãy giải thích xem tại sao với cách làm trên các mảnh có thể xếp vừa khít với miền diện tích trên cạnh b..
Cách 2:
Dựng hình và kiểm tra
1. Dựng đoạn thẳng AB.
2. Vẽ trung điểm D của đoạn thẳng này
3. Vẽ đường tròn bán kính DA.
4. Vẽ đoạn BC và AC , với C là một điểm nằm trên đường tròn. Như vvậy ta đã dựng được tam giác vuông ABC vuông tại C.
5. Vẽ các hình vuông trên các cạnh của tam giác vuông ABC.
6. Vẽ các trung điểm L, M, N của các cạnh phía ngoài của các hình vuông.
7. Vẽ các đoạn DL, DM, DL.
8. Vẽ đoạn FG, Vẽ tia DC, và điểm P là giao điểm cuat tia DC và đoạn FG, sau đó làm ẩn đi tia DC và hiện đoạn DP.
9. Tô màu khác nhau cho diện tích các tam giác DCF, DCG, và DBK.
Cách chứng minh này đưa ra mối liên quan giữa diện tích của các hình tam giác được tô màu với diện tích của các hình vuông trên các cạnh tam giác vuông.
Chọn menu Measure --> calculate để tính được tỉ lệ diện tích của các tam giác với các hình vuông tương ứng.
10. Đo diện tích các tam giác, và di chuyển điểm C quanh một nửa đường tròn trên đường kính AB.
Ta nhận thấy: tổng diện tích của 2 tam giác nhỏ luôn bằng diện tích của tam giác lớn hơn. Và tổng diện tích này không đổi khi điểm C chuyển động trên đường tròn. (xem hình bên dưới).
Cách 2:
Chứng minh:
Xép các tam giác vuông như hình vẽ:
Ta có: Tứ giác ABED là hình thang vuông, tam giác BCE là tam giác vuông cân.
\(S_{ABED}=2.S_{ABC}+S_{BCE}\)
\(\Leftrightarrow\dfrac{\left(b+c\right).\left(b+c\right)}{2}=2.\dfrac{bc}{2}+\dfrac{a^2}{2}\)
Rút gọn cả hai vế cho \(\dfrac{1}{2}\):
\(\Leftrightarrow\left(b+c\right).\left(b+c\right)=2.bc+a^2\)
\(\Leftrightarrow\left(b+c\right)^2=2.bc+a^2\)
\(\Leftrightarrow b^2+2.bc+c^2=2.bc+a^2\)
Rút gọn cả hai vế cho 2.bc:
\(\Leftrightarrow b^2+c^2=a^2\) (đpcm)
Cách 2:Ghép hình
Xếp các tam giác vuông bằng nhau như hình vẽ:
Đặt \(HE=a;AE=b;AH=c\)
Ta có:
\(S_{EFGH}=S_{MNPQ}+4.S_{AEH}\)
\(\Rightarrow a^2=\left(c-b\right)^2+4.\dfrac{bc}{2}\left(1\right)\)
\(S_{EFGH}=S_{ABCD}-4.S_{AEH}\)
\(\Rightarrow a^2=\left(b+c\right)^2-4.\dfrac{bc}{2}\left(2\right)\)
Công (1) và (2) ta có:
\(2a^2=\left(c-b\right)^2+\left(b+c\right)^2+4.\dfrac{bc}{2}-4.\dfrac{bc}{2}\)
\(\Rightarrow2a^2=c^2-2cb+b^2+b^2+2cb+c^2\)
\(\Rightarrow2a^2=2\left(b^2+c^2\right)1\Rightarrow a^2=b^2+c^2\)
hay \(HE^2=AE^2+AH^2\)(đpcm)
Kẻ \(AH\perp BC\) ( \(H\in BC\) )
Áp dụng hệ thức lượng vào \(\Delta ABC\) có \(\widehat{A}=90^o\):
+ \(AB^2=BH.BC\)
+ \(AC^2=CH.BC\)
=> \(AB^2+AC^2=BH.BC+CH.BC=\left(BH+CH\right).BC=BC^2\)
=> đpcm
Giải:
Vẽ tam giác ABC vuông tại A, kẻ \(AH\perp BC\)
Ta có: \(\widehat{C}+\widehat{A_2}=90^o\left(\widehat{H}=90^o\right)\)
\(\widehat{A_1}+\widehat{A_2}=90^o\)
\(\Rightarrow\widehat{C}=\widehat{A_1}\)
Tương tự, \(\widehat{B}=\widehat{A_2}\)
Xét \(\Delta AHC,\Delta BAC\) có:
\(\widehat{AHC}=\widehat{BAC}=90^o,\widehat{B}=\widehat{A_2}\left(cmt\right)\)
\(\Rightarrow\Delta HAC\)\(\sim\)\(\Delta HBA\left(g-g\right)\)
Tương tự, \(\Delta AHC\)\(\sim\)\(\Delta BAC\left(g-g\right)\) và
\(\Delta AHB\)\(\sim\)\(\Delta CAB\left(g-g\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{AC}{BC}=\dfrac{HC}{AC}\\\dfrac{AB}{BC}=\dfrac{HB}{AB}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}AC^2=HC.BC\\AB^2=HB.BC\end{matrix}\right.\)
\(\Rightarrow AB^2+AC^2=HC.BC+HB.BC\)
\(\Rightarrow AB^2+AC^2=\left(HC+HB\right)BC\)
\(\Rightarrow AB^2+AC^2=BC^2\)
\(\Rightarrowđpcm\)
Sau đây là cách chứng minh của James Abram Garfield: Sau đây là hình minh họa :

Mô tả : cho \(\Delta ABC\) và \(\Delta BDE\) có các cạnh bằng nhau nên 2 tam giác này bằng nhau.
+> \(\widehat{DBE}=\widehat{ACB}\) ,Mà \(\widehat{ACB}+\widehat{ABC}=90^o\Rightarrow\widehat{DBE}+\widehat{ABC}=90^o\)
+> \(\Delta CBE\) vuông tại B.
Ta có : SACEB\(=\dfrac{\left(a+b\right)\left(a+b\right)}{2}=\dfrac{a^2+2ab+b^2}{2}\)
SACB\(=S_{BDE}\)\(=\dfrac{ab}{2}\)
SCBE\(=\dfrac{c^2}{2}\)
Lại có : \(S_{ACEB}=S_{ACB}+S_{BDE}+S_{CBE}\)
Hay \(\dfrac{a^2+2ab+b^2}{2}=\dfrac{2ab}{2}+\dfrac{c^2}{2}=\dfrac{2ab+c^2}{2}\)
Suy ra \(\dfrac{a^2+b^2}{2}=\dfrac{c^2}{2}\Rightarrow a^2+b^2=c^2\)
+>> ĐPCM.
Đây là một cách hay mà Garfield đã phát hiện ra trong năm 1876.
Cách 3:
Chứng minh:
Tam giác ABC, AH vuông góc với BC
Ta có các tam giác vuông ABC, HAC, HBA đồng dạng
\(\Rightarrow AB^2=BC.BH\) và \(AC^2=BC.HC\)
\(\Leftrightarrow AB^2+AC^2=BC.BH+BC.HC\)
\(\Leftrightarrow AB^2+AC^2=BC.\left(BH+HC\right)\)
\(\Leftrightarrow AB^2+AC^2=BC.BC\)
\(\Leftrightarrow AB^2+AC^2=BC^2\left(đpcm\right)\)
Cách3: Ghép hình
Xếp các tam giác vuông bằng nhau như trên hình vẽ.
\(\Rightarrow ABCD\)là hình thang
\(\Rightarrow S_{ABCD}=\dfrac{\left(2b+2c\right).\left(b+c\right)}{2}\)
\(\Rightarrow S_{ABCD}=\left(b+c\right)^2\left(1\right)\)
Mặt khác:
\(S_{ABG}+S_{AGD}+S_{BGC}+S_{CDG}=S_{ABCD}\)
\(\Rightarrow S_{ABCD}=\dfrac{2bc}{2}+\dfrac{2bc}{2}+\dfrac{a^2}{2}+\dfrac{a^2}{2}=2bc+a^2\left(2\right)\)
Từ (1) và (2) suy ra:
\(\left(b+c\right)^2=2bc+a^2\Rightarrow b^2+2bc+2c^2=2bc+a^2\)
\(\Rightarrow a^2=b^2+c^2\)
hay \(AG^2=AE^2+EG^2\)(đpcm)
Theo hình vẽ, ta dễ chứng minh \(\widehat{BEC}\) vuông
Ta có: \(S_{ABCD}=\dfrac{\left(a+b\right)\left(a+b\right)}{2}=\dfrac{\left(a+b\right)^2}{2}\)
\(S_{ABE}=S_{DEC}=\dfrac{ab}{2}\Rightarrow S_{ABE}+S_{DEC}=2.\dfrac{ab}{2}=ab\)
\(S_{BEC}=\dfrac{c.c}{2}=\dfrac{c^2}{2}\)
Mà \(S_{ABCD}=S_{ABE}+S_{DEC}+S_{BEC}\Rightarrow S_{BEC}=S_{ABCD}-S_{ABE}-S_{DEC}\)
\(\dfrac{\Rightarrow c^2}{2}=\dfrac{\left(a+b\right)^2}{2}-ab\Rightarrow\dfrac{c^2}{2}=\dfrac{a^2+b^2+2ab}{2}-\dfrac{2ab}{2}\)
\(\Rightarrow\dfrac{c^2}{2}=\dfrac{a^2+b^2}{2}\Rightarrow c^2=a^2+b^2\)
Mà a,b là 2 cạnh góc vuông, c là cạnh huyền của 1 tam giác vuông
=> đpcm
Cách 4:
Chứng minh:
Kẻ đường thẳng qua B vuông góc với BC cắt AC ở D
Ta có: \(S_{ABD}+S_{ABC}=S_{BDC}\)
\(AB.AD+AB.AC=BD.BC\) (*)
Do \(AB^2=AD.AC\Rightarrow AD=\dfrac{AB^2}{AC}\)
\(\Delta ABD\) và \(\Delta BDC\) đồng dạng \(\Rightarrow AB.DC=BD.BC\Rightarrow BD=\dfrac{AB.DC}{BC}\)
Thay vào (*) ta được: \(AB.\left(\dfrac{AB^2}{AC}\right)+AB.AC=BC.\left(\dfrac{AB.DC}{BC}\right)\)
\(\Leftrightarrow\dfrac{AB^2}{AC}+AC=DC\)
\(\Leftrightarrow AB^2+AC^2=DC.AC\)
\(\Leftrightarrow AB^2+AC^2=BC^2\left(đpcm\right)\)
Nhìn vào hình vẽ thì \(a^2+b^2=c^2\) (9+16=25)
=> đpcm

Định lý có thể chứng minh bằng phương pháp đại số khi sử dụng 4 tam giác vuông bằng nhau có các cạnh a, b và c, các tam giác này được sắp xếp thành một hình vuông lớn có cạnh là cạnh huyền c.[1] Các tam giác bằng nhau có diện tích {\displaystyle {\tfrac {1}{2}}ab}, khi đó hình vuông nhỏ bên trong có cạnh là b − a và diện tích là (b − a)2. Diện tích của hình vuông lớn là:
{\displaystyle (b-a)^{2}+4{\frac {ab}{2}}=(b-a)^{2}+2ab=a^{2}+b^{2}.\,}
Vì hình vuông lớn có cạnh là c và có diện tích c2, nên
{\displaystyle c^{2}=a^{2}+b^{2}.\,}
Một cách chứng minh tương tự là sắp xếp 4 hình tam giác vuông trên xung quanh một hình vuông có cạnh là 'c (hình dưới).[2] Kết quả tạo ra một hình vuông lớn hơn có cạnh là a + b và diện tích (a + b)2. Tổng diện tích 4 tam giác và hình vuông có cạnh c bằng với diện tích của hình vuông lớn hơn,
{\displaystyle (b+a)^{2}=c^{2}+4{\frac {ab}{2}}=c^{2}+2ab,\,}
ta có:
{\displaystyle c^{2}=(b+a)^{2}-2ab=a^{2}+b^{2}.\,}
 Biểu đồ chứng minh của Garfield
Biểu đồ chứng minh của Garfield
Một phương pháp chứng minh nữa do cựu tổng thống Mỹ James A. Garfield đưa ra.[3][4] Thay vì sử xếp thành hình vuông, ông sử dụng hình thang, hình thang này có thể xây dựng từ hình vuông theo cách chứng minh thứ 2 ở trên bằng cách cắt thành 2 hình thang dọc theo đường chéo của hình vuông bên trong. Diện tích của hình thang bằng 1/2 diện tích của hình vuông lớn:
{\displaystyle {\frac {1}{2}}(b+a)^{2}.}
Hìng vuông bên trong tương tự cũng giảm đi 1/2, và chỉ có 2 tam giác khi đó các bước chứng minh có thể tính tương tự như trên trừ hệ số {\displaystyle {\frac {1}{2}}}, hệ số này đã bị loại ra bằng cách nhân 2 để thu được kết quả.
Chứng minh bằng vi phân[sửa | sửa mã nguồn]Cách chứng minh này bằng cách thay đổi cạnh huyền và sử dụng vi tích phân.[5][6][7]
Tam giác ABC là một tam giác vuông với BC là cạnh huyền. Chiều dài cạnh huyền là y, cạnh AC là x và cạnh AB là a.
 Hình vẽ chứng minh bằng vi phân
Hình vẽ chứng minh bằng vi phân
Nếu x gia tăng một lượng dx bằng cách kéo dài đoạn AC về phía D, thì y cũng tăng một lượng là dy. Hai cạnh này cũng thuộc tam giác CDE, cũng là một tam giác tương tự ABC. Do đó các tỉ số cạnh của chúng phải bằng nhau:
{\displaystyle {\frac {dy}{dx}}={\frac {x}{y}}.}
Công thức trên có thể được viết lại như sau:
{\displaystyle y\cdot dy-x\cdot dx=0.\,}
Đây là hàm vi phân với đáp án giải ra là
{\displaystyle y^{2}-x^{2}=C,\,}
Và hằng số có C có thể tìm được bằng cách cho x = 0 thì y = a, ta được phương trình
{\displaystyle y^{2}=x^{2}+a^{2}\,}
Dùng hình mở rộngCho hình tam giác vuông ABC.Gọi 3 cạnh của tam giác ABC là a,b và c. Nếu c là cạnh huyền của tam giác vuông ABC thì: {\displaystyle a^{2}+b^{2}=c^{2}}
 Diagram of the two algebraic proofs
Diagram of the two algebraic proofs
Định lý có thể chứng minh bằng phương pháp đại số khi sử dụng 4 tam giác vuông bằng nhau có các cạnh a, b và c, các tam giác này được sắp xếp thành một hình vuông lớn có cạnh là cạnh huyền c.] Các tam giác bằng nhau có diện tích {\displaystyle {\tfrac {1}{2}}ab}, khi đó hình vuông nhỏ bên trong có cạnh là b − a và diện tích là (b − a)2. Diện tích của hình vuông lớn là:
{\displaystyle (b-a)^{2}+4{\frac {ab}{2}}=(b-a)^{2}+2ab=a^{2}+b^{2}.\,}Vì hình vuông lớn có cạnh là c và có diện tích c2, nên
{\displaystyle c^{2}=a^{2}+b^{2}.\,}Một cách chứng minh tương tự là sắp xếp 4 hình tam giác vuông trên xung quanh một hình vuông có cạnh là 'c (hình dưới).Kết quả tạo ra một hình vuông lớn hơn có cạnh là a + b và diện tích (a + b)2. Tổng diện tích 4 tam giác và hình vuông có cạnh c bằng với diện tích của hình vuông lớn hơn,
{\displaystyle (b+a)^{2}=c^{2}+4{\frac {ab}{2}}=c^{2}+2ab,\,}ta có:
{\displaystyle c^{2}=(b+a)^{2}-2ab=a^{2}+b^{2}.\,} Biểu đồ chứng minh của Garfield
Biểu đồ chứng minh của Garfield
Một phương pháp chứng minh nữa do cựu tổng thống Mỹ James A. Garfield đưa ra. Thay vì sử xếp thành hình vuông, ông sử dụng hình thang, hình thang này có thể xây dựng từ hình vuông theo cách chứng minh thứ 2 ở trên bằng cách cắt thành 2 hình thang dọc theo đường chéo của hình vuông bên trong. Diện tích của hình thang bằng 1/2 diện tích của hình vuông lớn:
{\displaystyle {\frac {1}{2}}(b+a)^{2}.}Hìng vuông bên trong tương tự cũng giảm đi 1/2, và chỉ có 2 tam giác khi đó các bước chứng minh có thể tính tương tự như trên trừ hệ số {\displaystyle {\frac {1}{2}}}, hệ số này đã bị loại ra bằng cách nhân 2 để thu được kết quả.
Chứng minh bằng vi phânCách chứng minh này bằng cách thay đổi cạnh huyền và sử dụng vi tích phân.
Tam giác ABC là một tam giác vuông với BC là cạnh huyền. Chiều dài cạnh huyền là y, cạnh AC là x và cạnh AB là a.
 Hình vẽ chứng minh bằng vi phân
Hình vẽ chứng minh bằng vi phân
Nếu x gia tăng một lượng dx bằng cách kéo dài đoạn AC về phía D, thì y cũng tăng một lượng là dy. Hai cạnh này cũng thuộc tam giác CDE, cũng là một tam giác tương tự ABC. Do đó các tỉ số cạnh của chúng phải bằng nhau:
{\displaystyle {\frac {dy}{dx}}={\frac {x}{y}}.}Công thức trên có thể được viết lại như sau:
{\displaystyle y\cdot dy-x\cdot dx=0.\,}Đây là hàm vi phân với đáp án giải ra là
{\displaystyle y^{2}-x^{2}=C,\,}Và hằng số có C có thể tìm được bằng cách cho x = 0 thì y = a, ta được phương trình
{\displaystyle y^{2}=x^{2}+a^{2}\,}Đây là cách chứng minh định lí Py -ta-g bằng vật lý
Nào, mọi người hãy chuẩn bị một bể cá hình lăng trụ đáy là tam giác vuông có ba cạnh là a, b, c. Cái bể cá này có thể quay dễ dàng quanh một trục thẳng đứng đi qua một đỉnh của cạnh huyền tam giác.

Xong rồi chứ. Giờ thì đổ nước vào bể nhé, không nhất thiết phải đổ đầy bể đâu. Khi bể cá chứa nước, sẽ xuất hiện áp suất nước tác động lên đơn vị dài các cạnh của đáy bể. Mọi người đều biết áp suất này là như nhau. Ta cứ giả sử áp suất này là 1 (N/m) (N/m vì đây là áp suất lên đơn vị chiều dài các cạnh của thành bể). Các bạn có thể giả sử như vậy vì nếu không, có thể đổ lượng nước thích hợp để áp suất đó đúng là 1.
Mọi người quan sát cái đáy bể hình tam giác này nhé:

Áp lực nước tác động lên cạnh huyền có điểm đặt tại trung điểm và độ lớn bằng c.1 và bằng c (áp lực bằng áp suất trên đơn vị độ dài nhân với độ dài). Tương tự như vậy ta cũng xác định được áp lực tác động lên 2 cạnh còn lại lần lượt là a và b. Áp lực lên cạnh huyền gây ra tác động làm cái bể cá quay theo chiều ngược chiều kim đồng hồ trong khi hai áp lực kia làm bể cá quay theo chiều ngược lại. Như ta đã biết trong vật lý để đặc trưng cho khả năng làm quay vật của một lực nguời ta đưa ra đại lượng momen của lực. Momen này sẽ bằng độ lớn lực nhân với cánh tay đòn (À, cánh tay đòn là khoảng cách từ tâm quay P đến phương của lực).
Chẳng hạn với áp lực tác động lên cạnh huyền, momen của lực này là:
Momen này, nhắc lại có tác động làm vật quay theo chiều ngược kim đồng hồ. Tương tự như vậy, tổng momen của 2 áp lực kia là:
sẽ gây ra tác động làm vật quay theo chiều ngược lại (chiều kim đồng hồ).
Mà sự thật là cái bể cá đứng im re không hề quay. Nếu bạn nào không tin mà lại cũng không thể làm thực nghiệm kiểm chứng thì hãy thử nghĩ mà xem: Nếu cái bể cá đặt nằm ngang như thế mà tự mình cứ quay vòng vòng thì chúng ta có một cái động cơ vĩnh cửu mất rồi :). Các bạn cũng tin là không có động cơ vĩnh cửu chứ, thế nên chúng ta thống nhất là cái bể cá sẽ không quay. Nó không quay chứng tỏ rằng tổng các momen làm nó quay theo chiều ngược kim đồng hồ phải bằng tổng các momen làm nó quay theo chiều ngược lại. Vậy là:
hay
Một tam giác vuông là một tam giác có một góc vuông; các cạnh kề của nó là các cạnh tạo nên góc vuông; cạnh huyền là cạnh đối diện với góc vuông. Trong hình vẽ dưới, a và b là các cạnh kề, c là cạnh huyền:
![[IMG]](http://upload.wikimedia.org/wikipedia/commons/thumb/d/d2/Pythagorean.svg/250px-Pythagorean.svg.png)
Pytago đã phát biểu định lý mang tên ông trong cách nhìn của hình học phẳng thông qua:
Diện tích hình vuông tím bằng tổng diện tích hình vuông đỏ và xanh lam.
Tương tự, quyển Sulbasutra chép:
Một dây thừng nối dọc đường chéo hình chữ nhật tạo ra một diện tích bằng tổng diện tích tạo ra từ cạnh ngang và cạnh dọc của hình chữ nhật đó.
Dùng đại số sơ cấp hay hình học đại số, có thể viết định lý Pytago dưới dạng hiện đại, chú ý rằng diện tích một hình vuông bằng bình phương độ dài của cạnh hình vuông đó:
Nếu một tam giác vuông có cạnh kề dài bằng a và b và cạnh huyền dài c, thì
Cách chứng minh của Euclid
Lưu ý: Cái này mk lấy từ Wikipedia tiếng Anh, phải có công đoạn dịch nên mk có chỉnh sửa nhiều chỗ:

Vẽ \(\Delta\)ABC vuông tại A
Trên mỗi cạnh BC, AB và CA, vẽ các hình vuông CBDE, BAGF và ACIH
Từ A, vẽ một đường thẳng song song với BD. Nó sẽ cắt BC và DE lần lượt tại K và L.
Nối CF, AD, EA, BI, ta có các tam giác BCF , BDA, IBC, ACE.
Chứng minh:
Vì \(\left\{{}\begin{matrix}AL\text{//}BD\\BD\text{//}CE\end{matrix}\right.\Rightarrow AL\text{//}CE\)
Vì \(\left\{{}\begin{matrix}AL\text{//}BD\\BD\perp DE\end{matrix}\right.\Rightarrow AL\text{ }\perp DE\)
\(\Rightarrow\)BKLD là hình chữ nhật(dấu hiệu 1)
\(\Rightarrow\)EKLC là hình chữ nhật(dấu hiệu 1)
\(\widehat{CAB}\) và \(\widehat{BAG}\) đều là góc vuông; mà \(\widehat{CAG}=\widehat{CAB}+\widehat{BAG}=90^o+90^o=180^o\) nên C, A và G cùng nằm trên một đường thẳng . \(\widehat{BAC}\) và \(\widehat{CAH}\) đều là góc vuông; mà \(\widehat{BAH}=\widehat{BAC}+\widehat{CAH}=90^o+90^o=180^o\) nên B, A và H cùng nằm trên một đường thẳng .
\(\widehat{CBD}\) và \(\widehat{FBA}\) đều là góc vuông
\(\Rightarrow\widehat{CBD}=\widehat{FBA}\\ \Rightarrow\widehat{CBD}+\widehat{ABC}=\widehat{FBA}+\widehat{ABC}\\ \Leftrightarrow\widehat{DBA}=\widehat{FBC}\)
Xét \(\Delta DBA\) và \(\Delta FBC\)
\(\widehat{DBA}=\widehat{FBC}\) (chứng minh trên)
AB = FB(cạnh của cùng một hình vuông)
BD = BC(cạnh của cùng một hình vuông)
\(\Rightarrow\Delta DBA=\Delta FBC\)
Từ A-K-L là một đường thẳng song song với CE nên \(\Delta ACE\) và hình chữ nhật CELK có cùng chiều cao CK, cạnh đáy CE
\(S_{ACE}=\dfrac{CE\cdot CK}{2};S_{CELK}=CE\cdot CK\\ \Rightarrow S_{ACE}=\dfrac{1}{2}\cdot S_{CELK}\)
Từ C-A-G là một đường thẳng song song với BF nên \(\Delta FBC\) và hình chữ nhật BAGF(hình vuông là hình chữ nhật đặc biệt) có cùng chiều cao BA, cạnh đáy BF
\(S_{FBC}=\dfrac{BA\cdot BF}{2};S_{BAGF}=BA\cdot BF\\ \Rightarrow S_{FBC}=\dfrac{1}{2}\cdot S_{BAGF}\)
\(\Delta DBA=\Delta FBC\\ \Rightarrow S_{DBA}=S_{FBC}\\ \Leftrightarrow\dfrac{1}{2}\cdot S_{BDLK}=\dfrac{1}{2}\cdot S_{BAGF}\\ \Leftrightarrow S_{BDLK}=S_{BAGF}\\ \Leftrightarrow S_{BDLK}=BA^2\left(1\right)\)
\(\widehat{ACI}\) và \(\widehat{ECB}\) đều là góc vuông
\(\Rightarrow\widehat{ACI}=\widehat{ECB}\\ \Rightarrow\widehat{ACI}+\widehat{ACB}=\widehat{ECB}+\widehat{ACB}\\ \Leftrightarrow\widehat{ICB}=\widehat{ACE}\)
Xét \(\Delta ICB\) và \(\Delta ACE\)
\(\widehat{ICB}=\widehat{ACE}\)(chứng minh trên)
IC = AC(cạnh của cùng một hình vuông)
BC = EC(cạnh của cùng một hình vuông)
\(\Rightarrow\Delta ICB=\Delta ACE\)
Từ A-K-L là một đường thẳng song song với CE nên \(\Delta CEA\) và hình chữ nhật CELK có cùng chiều cao CK, cạnh đáy CE
\(S_{CEA}=\dfrac{CE\cdot CK}{2};S_{CELK}=CE\cdot CK\\ \Rightarrow S_{CEA}=\dfrac{1}{2}\cdot S_{CELK}\)
Từ B-A-H là một đường thẳng song song với IC nên \(\Delta IBC\) và hình chữ nhật ICAH(hình vuông là hình chữ nhật đặc biệt) có cùng chiều cao CA, cạnh đáy IC
\(S_{IBC}=\dfrac{CA\cdot IC}{2};S_{ICAH}=CA\cdot IC\\ \Rightarrow S_{IBC}=\dfrac{1}{2}\cdot S_{ICAH}\)
\(\Delta ICB=\Delta ACE\\ \Rightarrow S_{ICB}=S_{ACE}\\ \Leftrightarrow\dfrac{1}{2}\cdot S_{CELK}=\dfrac{1}{2}\cdot S_{ICAH}\\ \Leftrightarrow S_{CELK}=S_{ICAH}\\ \Leftrightarrow S_{CELK}=CA^2\left(2\right)\)
Cộng vế theo vế (1) và (2) ta có: \(S_{BDLK}+S_{CELK}=BA^2+CA^2\\ BD\cdot BK+CE\cdot CK=BA^2+CA^2\)
Vì BD = CE (cùng là cạnh của một hình vuông) nên
\(BD\cdot BK+BD\cdot CK=BA^2+CA^2\\ BD\left(BK+CK\right)=BA^2+CA^2\\ BD\cdot BC=BA^2+CA^2\)
Vì BD = BC (cùng là cạnh của một hình vuông) nên
\(BC\cdot BC=BA^2+CA^2\\ \Leftrightarrow BC^2=BA^2+CA^2\left(ĐPCM\right)\)
Có nhiều cách cắt, ghép hình thể hiện định lý Pytago:
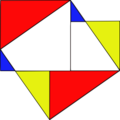

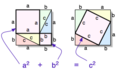

Dựng hình và kiểm tra
1. Vẽ một tam giác vuông và các hình vuông trên các cạnh của nó (dùng công cụ custom)
2. Kéo dài tia HA, lấy điểm A’ đối xứng với điểm H qua A bằng cách :
+ Chọn đoạn HA và điểm A
+ Chọn menu Transform --> Rotate --> degrees =180
3. Vẽ một đường thẳng đi qua điểm B và vuông góc với đoạn AA’, Vẽ điểm giao K của 2 đường này.
( Hình bên minh họa cho các bước từ 1 đến 3)
4. Vẽ hình vuông A’KLM.
(Sử dụng công cụ Custom tool như đã giới thiệu ở bài 1)
5. Vẽ Đoạn BK, GM, FL.
6. Làm ẩn đi đường BK.
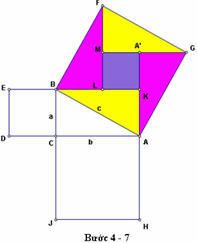
7. Tô màu cho 4 mảnh trong hình vuông trên cạnh huyền.
8. Đánh dấu vectơ EJ và dịch chuyển 4 đỉnh và 4 cạnh của hình vuông BCDE theo vectơ này (để được hình vuông bên dưới hình vuông trên cạnh b có diện tích bằng diện tích hình vuông BCDE )
+ Đánh dấu theo thứ tự điểm E, J
+ Chọn menu Transform --> Mark vector
+ Đánh dấu 4 cạnh và 4 đỉnh của hình vuông BCDE
+ Chọn vào Menu Transform --> Translate.
9. Như vậy miền diện tích trên cạnh b bây giờ là a2 + b2 . Sử dụng công cụ Translator để di chuyển các các mảnh là bản sao của các mảnh trong hình
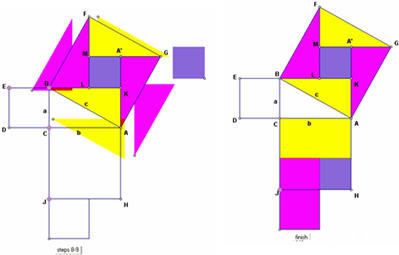
vuông trên cạnh huyền vào trong miền có diện tích a2 + b2 trên cạnh b.
Cách 6:
Chứng minh:
Trên BC lấy D, E sao cho: CD = CE = CA = b
\(\Rightarrow\Delta ADE\) vuông ở A (vì có \(AC=\dfrac{DE}{2}\), CD = CE)
Ta có: \(\Delta BAD~\Delta BEA\left(g.g\right)\) (Vì có \(\widehat{B}\) chung và \(\widehat{BAD}=\widehat{EAC}=\widehat{E}\))
\(\Rightarrow\dfrac{BA}{BE}=\dfrac{BD}{BA}\Leftrightarrow\dfrac{c}{a+b}=\dfrac{a-b}{c}\)
\(\Leftrightarrow c^2=\left(a-b\right)\left(a+b\right)\)
\(\Leftrightarrow c^2=a^2-b^2\)
\(\Leftrightarrow c^2+b^2=a^2\left(đpcm\right)\)
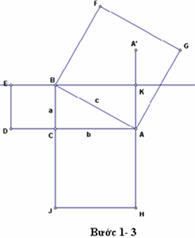
Dựng hình và kiểm tra
1. Vẽ một tam giác vuông và các hình vuông trên các cạnh của nó (dùng công cụ custom)
2. Kéo dài tia HA, lấy điểm A’ đối xứng với điểm H qua A bằng cách :
+ Chọn đoạn HA và điểm A
+ Chọn menu Transform --> Rotate --> degrees =180
3. Vẽ một đường thẳng đi qua điểm B và vuông góc với đoạn AA’, Vẽ điểm giao K của 2 đường này.
( Hình bên minh họa cho các bước từ 1 đến 3)
4. Vẽ hình vuông A’KLM.
(Sử dụng công cụ Custom tool như đã giới thiệu ở bài 1)
5. Vẽ Đoạn BK, GM, FL.
6. Làm ẩn đi đường BK.

7. Tô màu cho 4 mảnh trong hình vuông trên cạnh huyền.
8. Đánh dấu vectơ EJ và dịch chuyển 4 đỉnh và 4 cạnh của hình vuông BCDE
theo vectơ này (để được hình vuông bên dưới hình vuông trên cạnh b có
diện tích bằng diện tích hình vuông BCDE )
+ Đánh dấu theo thứ tự điểm E, J
+ Chọn menu Transform --> Mark vector
+ Đánh dấu 4 cạnh và 4 đỉnh của hình vuông BCDE
+ Chọn vào Menu Transform --> Translate.
9. Như vậy miền diện tích trên cạnh b bây giờ là a2 + b2 . Sử dụng công cụ Translator để di chuyển các các mảnh là bản sao của các mảnh trong hình

Dựng hình và kiểm tra
1. Dựng đoạn thẳng AB.
2. Vẽ trung điểm D của đoạn thẳng này
3. Vẽ đường tròn bán kính DA.
4. Vẽ đoạn BC và AC , với C là một điểm nằm trên đường tròn. Như vvậy ta đã dựng được tam giác vuông ABC vuông tại C.
5. Vẽ các hình vuông trên các cạnh của tam giác vuông ABC.
6. Vẽ các trung điểm L, M, N của các cạnh phía ngoài của các hình vuông.
7. Vẽ các đoạn DL, DM, DL.
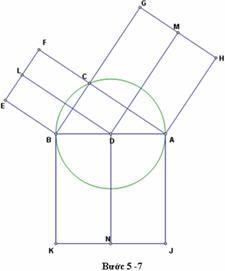
8. Vẽ đoạn FG, Vẽ tia DC, và điểm P là giao điểm cuat tia DC và đoạn FG, sau đó làm ẩn đi tia DC và hiện đoạn DP.
9. Tô màu khác nhau cho diện tích các tam giác DCF, DCG, và DBK.
Cách chứng minh này đưa ra mối liên quan giữa diện tích của các hình tam giác được tô màu với diện tích của các hình vuông trên các cạnh tam giác vuông.
Chọn menu Measure --> calculate để tính được tỉ lệ diện tích của các tam giác với các hình vuông tương ứng.
Chứng minh định lí Pi-ta-go bằng nhiều cách
VNMATH.COM14 THÁNG 2, 2012GIẢI TOÁN BẰNG NHIỀU CÁCH , HÌNH HỌC PHẲNG , TOÁN THCS1Chuyên đề 20 cách chứng minh định lý Py-ta-go (file word, viết dưới dạng sáng kiến kinh nghiệm). Download.
Chứng minh Định lí Pytago bằng cách ghép hình sưu tầm bởi thầy Nguyễn Phước, Huế.
Cách 1: Chứng minh của E. A. Coolidge
Cách chứng minh này xuất hiện trong cuốn sách về các vấn đề kinh điển thuộc học thuyết Pitago của tác giả Elisha Scott Loomis, được xuất bản lần đầu tiên bởi Hội đồng giáo viên quốc gia của môn toán học, vào năm 1927. Thật đáng tiếc, quyển sách này hiện nay không được xuất bản nữa, trong cuốn sách này có tới trên 300 cách chứng minh định lý Pitago, trong đó, có nhiều cách chứng minh tương tự nhau, và tất cả các cách chứng minh nổi tiếng đều có trong cuốn sách của Loomis.
Cách chứng minh dưới đây thì tương tự như cách chứng minh của Bhaskara trong phần “Behold!” đã giới thiệu ở bài trước. Cách chứng minh này được đăng trên tạp trí giáo dục, xuất bản hàng ngày, và tác giả của nó là cô E. A. Coolidge - là một người mù.

Dựng hình và kiểm tra
1. Vẽ một tam giác vuông và các hình vuông trên các cạnh của nó (dùng công cụ custom)
2. Kéo dài tia HA, lấy điểm A’ đối xứng với điểm H qua A bằng cách :
+ Chọn đoạn HA và điểm A
+ Chọn menu Transform --> Rotate --> degrees =180
3. Vẽ một đường thẳng đi qua điểm B và vuông góc với đoạn AA’, Vẽ điểm giao K của 2 đường này.
( Hình bên minh họa cho các bước từ 1 đến 3)
4. Vẽ hình vuông A’KLM.
(Sử dụng công cụ Custom tool như đã giới thiệu ở bài 1)
5. Vẽ Đoạn BK, GM, FL.
6. Làm ẩn đi đường BK.

7. Tô màu cho 4 mảnh trong hình vuông trên cạnh huyền.
8. Đánh dấu vectơ EJ và dịch chuyển 4 đỉnh và 4 cạnh của hình vuông BCDE
theo vectơ này (để được hình vuông bên dưới hình vuông trên cạnh b có
diện tích bằng diện tích hình vuông BCDE )
+ Đánh dấu theo thứ tự điểm E, J
+ Chọn menu Transform --> Mark vector
+ Đánh dấu 4 cạnh và 4 đỉnh của hình vuông BCDE
+ Chọn vào Menu Transform --> Translate.
9. Như vậy miền diện tích trên cạnh b bây giờ là a2 + b2 . Sử dụng công cụ Translator để di chuyển các các mảnh là bản sao của các mảnh trong hình

vuông trên cạnh huyền vào trong miền có diện tích a2 + b2 trên cạnh b.
Chú ý:
- Hãy thử thay đổi tam giác của bạn, và quan sát xem các mảnh tương ứng còn lại có bằng nhau nữa không.?
- Chú ý rằng, trong trương hợp dựng hình như thế này cạnh b cần phải luôn được giữ là cạnh bên dài hơn nếu không thì sự dựng hình như trên sẽ bị sai.
- Trường hợp đặc biệt trước khi việc dựng hình bi sai là trương hợp cạnh b dài bằng cạnh a thì hình vuông A’KLM biến mất.
- Bạn hãy giải thích xem tại sao với cách làm trên các mảnh có thể xếp vừa khít với miền diện tích trên cạnh b..
Cách 2: Chứng minh của Ann Condit
Đây cũng là một cách chứng minh được giới thiệu trong cuốn sách của Elisha Scott Loomis. Ann Condit nghĩ ra cách chứng minh này vào năm 1938 khi cô mới 16 tuổi và là sinh viên của trường trung học ở miền nam Ấn Độ.
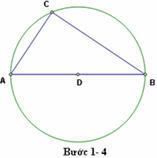
Dựng hình và kiểm tra
1. Dựng đoạn thẳng AB.
2. Vẽ trung điểm D của đoạn thẳng này
3. Vẽ đường tròn bán kính DA.
4. Vẽ đoạn BC và AC , với C là một điểm nằm trên đường tròn. Như vvậy ta đã dựng được tam giác vuông ABC vuông tại C.
5. Vẽ các hình vuông trên các cạnh của tam giác vuông ABC.
6. Vẽ các trung điểm L, M, N của các cạnh phía ngoài của các hình vuông.
7. Vẽ các đoạn DL, DM, DL.

8. Vẽ đoạn FG, Vẽ tia DC, và điểm P là giao điểm cuat tia DC và đoạn FG, sau đó làm ẩn đi tia DC và hiện đoạn DP.
9. Tô màu khác nhau cho diện tích các tam giác DCF, DCG, và DBK.
Cách chứng minh này đưa ra mối liên quan giữa diện tích của các hình tam giác được tô màu với diện tích của các hình vuông trên các cạnh tam giác vuông.
Chọn menu Measure --> calculate để tính được tỉ lệ diện tích của các tam giác với các hình vuông tương ứng.
10. Đo diện tích các tam giác, và di chuyển điểm C quanh một nửa đường tròn trên đường kính AB.
Ta nhận thấy: tổng diện tích của 2 tam giác nhỏ luôn bằng diện tích của tam giác lớn hơn. Và tổng diện tích này không đổi khi điểm C chuyển động trên đường tròn. (xem hình bên dưới).
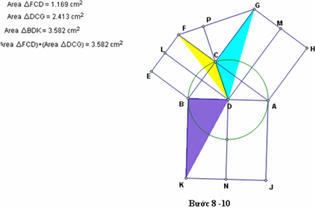
Nhận xét:
Bạn có thể đã phát hiện ra rằng tổng diện tích của 2 tam giác nhỏ luôn bằng diện tích của tam giác lớn hơn( DBK). Nếu bạn có thể chứng minh được điều này là đúng , và nếu bạn có thể liên hệ từ các diện tích này
Với diện tích của các hình vuông, thì bạn sẽ chưngd minh được định lý
Pitago. Sau đây là các bước gợi ý để giúp bạn chứng minh định lý.
1. Các tam giác DCG, DCF, và DBK cóchiều dài 1 cạnh bằng nhau đó là : DC và BD( cì đều bằng bán kính đườn tròn.
2. Đoạn PF và PG theo thứ tự là đường cao của 2 tam giác DCF và DCG.
3. Chỉ ra rằng dt DCG + dt DCF = dt DBK.
4. So sánh DCF, DCG, DBK theo thứ với diện tích của các hình vuông CFEB, CAHG, BAGK ?
5. Nếu bạn làm được những yêu cầu trên thì bạn đã chứng minh được định lý Pitago.
Cách 3: Chứng minh của Leonardo da Vinci
Leonardo da Vinci (1452 – 1519) là một họa sĩ lớn , một kỹ sư, và là một nhà phát minh lớn người Ý trong thời kỳ phục hưng. Ông nổi tiếng trong nhiều lĩnh vực khác nhau, và là tác giả của bức họa nổi tiếng nàng Mona Lisa. Ông cũng được tín nhiệm trong cách chứng minh định lý Pitago dưới
đây.
1. Vẽ một tam giác vuông và các hình vuông trên hai cạnh bên của nó.
(Trong hình này bạn không phải vẽ hình vuông trên cạnh huyền).
2. Bạn hãy nối hai đỉnh của hai hình vuông để vẽ được một tam giác vuông thứ hai bằng với tam giác vuông ABC ban đầu.
3. Hãy vẽ một đoạn thẳng đi qua tâm của hình này, đó chính là đoạn thẳng đi qua C và nối hai điỉnh xa nhất của 2 hình vuông (là đường nét đứt trên hình bên).
4. Hãy vẽ trung điểm D của đoạn này.
5. Quan sát hình chúng ta thấy rằng: đây chính là đoạn thẳng chia hình thành 2 phần đối xứng nhau . Chọn tất cả các đoạn thẳng và các điểm nằm ở một phía của đường thẳng này, và tạo một nút hoạt động Hide/Show để làm ẩn /hiện phần hình được đánh dấu này.
Đặt lại tên cho nút này là Hide Reflection.
6. Kích chuột vào nút Hide Reflection này và bạn sẽ thấy được một nửa hình của ban đầu, phần hình đối xứng với nó bị ẩn đi (như hình bên dưới).
7. Đánh dấu điểm D làm điểm tâm và quay toàn bộ hình này 180o quanh điểm D .
Như vậy chúng ta đã tạo ra một đa giác mới có diện tích đúng bằng diện tích của đa giác ban dầu.
8. Chọn đánh dấu tất cả các đối tượng ( đoạn thẳng và điểm) của phần
hình tạo được do xoay một nửa hình ban đầu và tạo1 nút hoạt động nữa.
Đặt tên cho nút này là Hide Rotation (xem hình bên dưới).
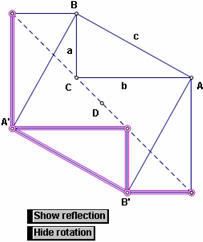
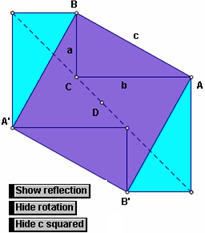
9. Vẽ đoạn A’B, và đoạn B’A. Như vậy chúng ta có thể dễ dàng nhận thấy tứ giác BA’B’A chính là hình vuông trên cạnh c
10. Tô màu cho diện tích của hình tứ giác BA’B’A và hai tam giác vuông liền kề nó.
11. Đánh dấu đoạn A’B, và đoạn B’A, và diện tích của 3 đa giác ( gồm 2 tam giác vuông và 1 hình tứ giác), và tạo thêm 1 nút hoạt động . Có tên là Hide c Squared.
Nhận xét: Từ các bước dựng hìnhnhư trên, chúng ta có thể hình dung được cách chứng minh định lý của Leonardo da Vinci:
+ Cách dựng hình ở bước 1 – 4 cho 1 đa giác có 2 nửa đối xứng nhau qua 1 dường thẳng. Đa giác này có diện tích bằng tổng diện tích của 2 hình vuông trên các cạnh bên a, b của tam giác vuông ABC và diện tích của 2 tam giác vuông( có độ dài 2 cạnh bên là a, b).
+ Khi xoay 1 nửa đa giác trên quanh điểm tâm D của đường phân cách 180o cho ta một đa giác mới có diện tích đúng bằng diện tích đa giác ba đầu.
+ Dựa vào hình vẽ ta thấy diện tích tứ giác BA’B’A = (a2 + b2 + 2ab) – 2ab = a2 + b2 (1)
+ Việc nối A với B’, B với A’ cho ta hình vuông BA’B’A. (Vì AB song song và bằng A’B’ ; A’B và AB’ cũng song song và bằng nhau ). Tứ giác BA’B’A chính là hình vuông có cạnh là c diện tích của hình vuông này là c2 (2)
Tử (1) và (2) ta có được c2 = a2 + b2 . Có nghĩa là định lý Pitago được chứng minh.
12. Hãy thử kích vào các nút Hide, sau đó lại kích lại vào chúng. Như vậy bạn sẽ thấy được sự biến đổi của các bước làm trên : từ 1 hình gồm 2 tam giác vuông và 2 hình vuông trên 2 cạnh bên biến đổi thành hình gồm 2 tam giác vuông và 1 hình vuông trên cạnh huyền của chúng. ( mà diện tích của toàn bộ hình không đổi). Đây chính là cách chứng minh định lý của daVinci.
Cách 4: Chứng minh của 1 tổng thống
James A. Garfield đã khám phá ra một cách chứng minh định lý Pitago vào
năm 1876, một vài năm trước khi ông ta trở tổng thống Hoa Kỳ. Một điều
thú vị là trong ngành toán học không chỉ có một người trở thành tổng
thống. Trước Garfield là ông Abraham Lincoln, là một thành viên của tổ
chức Euclid là một trong những tác giả của những cuốn sách có sức thuyết
phục nhất. Ông vừa là một luật sư vừa là một nhà chính trị. Cách chứng
minh của Garfield được minh họa với một hình tương dối đơn giản: là một
hình thang.
Dựng hình và kiểm tra .
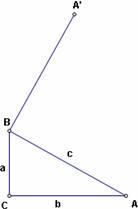
1. Vẽ một tam giác vuông ABC và đặt tên các đỉnh như hình bên.
2. Đánh dấu điểm B làm tâm và quay cạnh c và điểm A theo B một góc 90o .( sau bước này ta được hình bên)
3. Nối điểm A và A’ sau đó vẽ một đường thẳng đi qua A’ và song song với cạnh b.
4. Sử dụng công cụ Ray để kéo dài đoạn CB. Và vẽ điểm giao D cỉa của tia này với đường thẳng đi qua A’.
5. Làm ẩn đi tia và đường thẳng đi và thay vào đó là đoạn BD và DA’.
Như vậy ta có tứ giác ACDA’ là 1 hình thang vuông vì :
+ DA’ và CA song song( do cách dựng ở bước 3)
+ Góc ACB vuông( do ABC là tam giác vuông ban đầu) góc CDA’ vuông.
6. Tô màu đa giác theo 3 tam giác vuông bên trong nó.
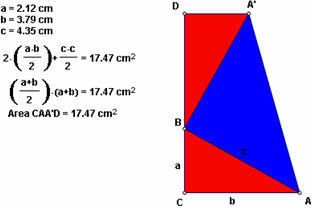
7. Hãy đo độ dài cạnh a, b, c.Và bạn có thể sử dụng kết quả đo lường này để tính toán diện tích của 3 tam giác và tổng của chúng :
+ Đo độ dài các cạnh bằng cách : di chuột đến cạnh đó và kích chuột phải length
+ Đo diện tích tam giác : kích chuột phải lên tam giác đó chọn Area
+ Tính tổng các tam giác : chọn menu Measure Calculate.
8. Sử dụng công thức tính diện tích của hình thanhg để tính diện tích hình ACDA’ chỉ dựa vào độ dài các cạnh.( dùng cái gì để đo chiều cao của hình thang vuông ?). Hãy vẽ miền trong đa giác của toàn bộ hình và xác nhận lại các tính toán của bạn đă làm là đúng.
- Trong cách chứng minh này từ cách dựng hình như trên , chúng ta tính được diện tích hình thang ACDA’ theo 2 cách :
Cách 1: Tính theo 3 tham số a, b, c (dựa vào hình vẽ ta thấy diện tích hình thang bằng tổng diện tích 3 tam giác vuông trong đó 2 tam giác vuông màu đỏ có diện tích bằng nhau do tính chất của phép quay) thì ta có :
Dt = 2*ab /2 + c*c /2 (1)
Cách 2: tính theo 2 tham số a. b(dựa vào công thức tính diện tích hình thang):
Dt = (a+ b) *(a+b)/2 (2)
Từ (1) và(2) ta có Dt =ab+ c2/2 = (a+b)2/2 c2 = a2 + b2. chính là điều phải chứng minh.
Cách 5: Chứng minh định lý Pitago của Perigal
- Có nhiều cách chứng minh định lý Pitagocó nguồn gốc từ cổ xưa, nhưng lại được chứng minh lại bởi những người không biết đến nguồn gốc cổ xưa của nó. Đây là một cách chứng minh mà được ’ khám phá’ ra bởi nhà toán học Henry Perigal vào năm 1873, nhưng cách chứng minh này lại được biết đến là cách chứng minh của nhà toán học người A- rập Tâbit ibn Qorra.a cách đó hàng nghìn năm.
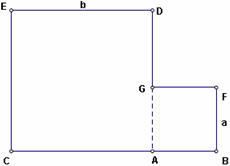
Dựng hình và kiểm tra
1. Vẽ một hình vuông CADE.
2. Vẽ một hình vuông nhỏ hơn sát ngay hình vuông CADE vừa vẽ sao cho 2 hình vuông này có chung một đỉnh( là A) và đỉnh thứ hai của hình vuông nhỏ nằm trên cạnh DA( đỉnh G) hình vuông nhỏ tạo được là hình vuông AGFB. Đặt tên cho độ dài cạnh của 2 hình vuông này lần lượt là b, a .
(hình bên minh họa cho bước 1 – 2).
3. Đánh dấu đoạn AB như 1 vectơ và dịch chuyển điểm C theo vectơ này. Cách làm như sau :
--> Chọn ( theo thứ tự) điểm A và điểm B, sau đó chọn Mark Vector từ menu Transform. Sau đó chọn chọn điểm C và chọn Translate từ menu Transform.
4. Vẽ đoạn thẳng EC’ và C’F.
5. Tô màu cho miền trong các đa giác là tam giác ( tam giác ECC’, và tam giác C’FB).
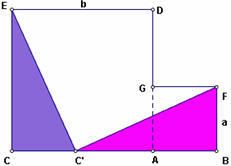
Nhận xét: Chúng ta bắt đầu dựng hình với 2 hình vuông liền kề với nhau, và bên trong của hình này chúng ta dựng hai tam giác vuông :
+ Trong tam giác vuông ECC’ ta có cạnh EC là cạnh hình vuông lớn nên có độ dài là b ; cạnh CC’ là kết quả của việc dịch chuyển điểm C theo vectơ AB nên CC’ dài bằng đoạn AB có độ dài là a.
 +
+Trong tam giác C’FB ta có cạnh FB là cạnh của hình vuông nhỏ, nên có độ dài là a. Cạnh C’B có độ dài bằng b ( Vì đoạn CC’ dài bằng đoạn AB).
--> Như vậy 2 tam giác vuông ECC’ và C’FB là 2 tam giác có diện tích bằng nhau là (a*b) /2.
Gọi độ dài cạnh huyền cuả tam giác vuông này là c.
6. Sử dụng công cụ Translator để chuyển dịch tam giác ECC’ từ điểm C đến điểm G , và để chuyển tam giác C’BF từ điểm B tới điểm D.(Xem lại bài tạo công cụ Translator đã giới thiệu) Việc dịch chuyển các tam giác không làm thay đổi kích thước của các tam giác đó.
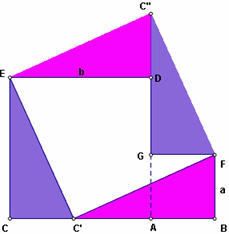
7. Đánh dấu điểm E làm tâm và quay điểm C’ một góc 90o để tạo thành hình vuông EC’FC’’.
Nhận xét:
- Vì EC là cạnh của tam giác vuông ECC’ nên hình vuông EC’FC’’ có diện tích là c2.
Vì tam giác vuông ECC’ được di chuyển thành tam giác C’’GF : góc ECC’ = góc C’’GF( = 90o ).
Cạnh CC’ = cạnh GF( = a).
Cạnh CE = cạnh GC’’( =b).
Diện tích tam giác ECC’’= diện tích tam giác C’’GB.
Tương tự ta có : Diện tích tam giác C’BF = diện tích tam giác EDC’’.
Vậy ta có diện tích của tứ giác EC’FC’’ băng tổng diện hai hình vuông có cạnh b, a ban đầu. Nên diện tích EC’FC’’ = a2 + b2.
Đồng thời vì EC’FC’’ cũng là hình vuông có độ dài cạnh bằng độ dài cạnh
huyền cuả tam giác vuông có các cạnh bên là b, a( dựng hình bước 7).
Nên diện tích của hình vuông EC’FC’’= c2 . Hay trong 1 tam giác vuông có c2= a2 + b2 (c là cạnh huyền, a,b là 2 cạnh bên).
Vậy có nghĩa là ta đã chứng minh được định lý Pitago.
Oa, xem xong cái này tự nhiên thấy toán học thiệt thú vị, trước đây mình chỉ biết mỗi cách cm cô vừa cho thui, chứ mik chưa bao giờ tìm hỉu thêm, Cảm thấy mik yêu toán hơn rất nhìu
Các bạn không được dẫn link mà phải trình bày đầy đủ ra mới có điểm.
Chẳng ai làm cách đường tròn cả :v
Vẽ đường tròn (D;a). Gọi BC là đường kính qua D.
Ta có:
\(BH=a-b;AD=CD=a;HC=a+b\)
Xét tam giác AHB và tam giác CHA ta có:
\(\widehat{AHB}=\widehat{CHA}\left(=90^o\right);\widehat{ABH}=\widehat{CAH}\)(cùng phụ với \(\widehat{BAH}\))
Do đó \(\Delta AHB\infty\Delta CHA\left(g.g\right)\)
\(\Rightarrow\dfrac{AH}{CH}=\dfrac{BH}{AH}\Rightarrow AH^2=CH.BH\)
\(\Rightarrow c^2=\left(a+b\right).\left(a-b\right)\Rightarrow c^2=a^2-b^2\)
\(\Rightarrow a^2=b^2+c^2\) hay \(AB^2=BH^2+AH^2\)(đpcm)
cái này trc e đọc toán tuổi thơ có hơi bị nhiều nè, số 42 thì phải :V, hình như thế

1. Vẽ một tam giác vuông và các hình vuông trên các cạnh của nó (dùng công cụ custom)
2. Kéo dài tia HA, lấy điểm A’ đối xứng với điểm H qua A bằng cách :
+ Chọn đoạn HA và điểm A
+ Chọn menu Transform --> Rotate --> degrees =180
3. Vẽ một đường thẳng đi qua điểm B và vuông góc với đoạn AA’, Vẽ điểm giao K của 2 đường này.
Cách 5:
Chứng minh:
Qua B dựng đường thẳng vuông góc với BC cắt AC tại C'
Dựng các hình bình hành ABCB', BC'CA'
\(\Rightarrow\Delta ABC=\Delta AB'C\)
\(S_{AB'C}+S_{ABC'}=S_{BCC'}=S_{BCA'}\)
\(\Leftrightarrow AB.AC+AB.AC'=BC.CA'\) (*)
Ta có: \(AC'=\dfrac{AB^2}{AC}\)
Và \(\Delta CA'B~\Delta ABC\Rightarrow CA'.CA=BA.BC\)
\(\Rightarrow CA'=\dfrac{BA.BC}{CA}\)
Thay vào (*) ta được:
\(AB.AC+AB.\dfrac{AB^2}{AC}=BC.\dfrac{BA.BC}{CA}\)
\(\Leftrightarrow AC+\dfrac{AB^2}{AC}=BC^2\)
\(\Leftrightarrow AC^2+AB^2=BC^2\left(đpcm\right)\).












 , khi đó hình vuông nhỏ bên trong có cạnh là b − a và diện tích là (b − a)2. Diện tích của hình vuông lớn là:
, khi đó hình vuông nhỏ bên trong có cạnh là b − a và diện tích là (b − a)2. Diện tích của hình vuông lớn là:




 , hệ số này đã bị loại ra bằng cách nhân 2 để thu được kết quả.
, hệ số này đã bị loại ra bằng cách nhân 2 để thu được kết quả.





















