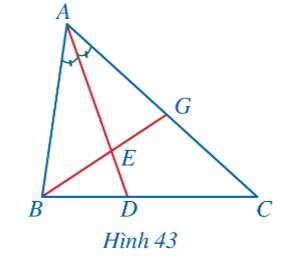
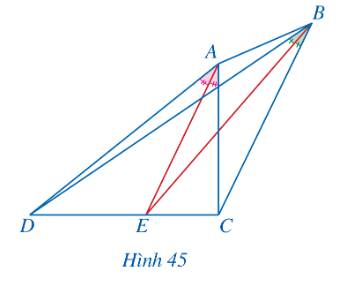
Xét tam giác ABC với ba đường phân giác AD, BE, CF, ta có:
\(\frac{{AB}}{{AC}} = \frac{{DB}}{{DC}};\,\,\frac{{BC}}{{BA}} = \frac{{EC}}{{EA}};\,\,\frac{{CA}}{{CB}} = \frac{{FA}}{{FB}}\) (Tính chất đường phân giác)
\( \Rightarrow \frac{{DB}}{{DC}}.\frac{{EC}}{{EA}}.\frac{{FA}}{{FB}} = \frac{{AB}}{{AC}}.\frac{{BC}}{{BA}}.\frac{{CA}}{{CB}} = \frac{{AB.BC.CA}}{{CA.AB.BC}} = 1\) (đpcm).