Xét tam giác ABC có AD là đường phân giác nên \(\frac{{AB}}{{AC}} = \frac{{DB}}{{DC}}\)
Mà \(AB < AC\)\( \Rightarrow \frac{{AB}}{{AC}} < 1 \Rightarrow \frac{{DB}}{{DC}} < 1 \Rightarrow DB < DC\).
Xét tam giác ABC có AD là đường phân giác nên \(\frac{{AB}}{{AC}} = \frac{{DB}}{{DC}}\)
Mà \(AB < AC\)\( \Rightarrow \frac{{AB}}{{AC}} < 1 \Rightarrow \frac{{DB}}{{DC}} < 1 \Rightarrow DB < DC\).
Cho tam giác ABC, điểm D thuộc cạnh BC sao cho \(\frac{{DB}}{{DC}} = \frac{{AB}}{{AC}}\). Chứng minh AD là tia phân giác của góc BAC.
Cho tam giác ABC, điểm D thuộc cạnh BC sao cho \(\frac{{DB}}{{DC}} = \frac{{AB}}{{AC}}\). Chứng minh AD là tia phân giác của góc BAC.
Cho tam giác ABC vuông tại A có AB = 3, AC = 4, AD là đường phân giác. Tính:
a) Độ dài các đoạn thẳng BC, DB, DC;
b) Khoảng cách từ điểm D đến đường thẳng AC;
c) Độ dài đường phân giác AD
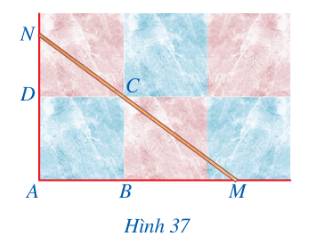
Trong Hình 38, tam giác ABC có AD là đường phân giác của góc BAC. Giả sử mỗi ô vuông của lưới ô vuông có độ dài cạnh bằng 1 cm.
a) Tính độ dài các đoạn thẳng DB, DC.
b) Tính độ dài các đoạn thẳng AB, AC.
c) So sánh các tỉ số \(\frac{{DB}}{{DC}},\,\,\frac{{AB}}{{AC}}\).
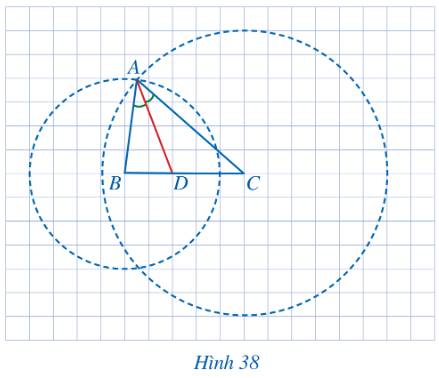
Quan sát Hình 43 và chứng minh \(\frac{{DB}}{{DC}}:\frac{{EB}}{{EG}} = \frac{{AG}}{{AC}}\)
Cho tam giác ABC có đường trung tuyến AM. Tia phân giác của góc ABC lần lượt cắt các đoạn thẳng AM, AC tại điểm D, E. Chứng minh \(\frac{{EC}}{{EA}} = 2\frac{{DM}}{{DA}}\).
Cho tam giác ABC có ba đường phân giácAD, BE, CF. Biết \(AB = 4,\,\,BC = 5,\,\,CA = 6\). Tính BD, CE, AF.
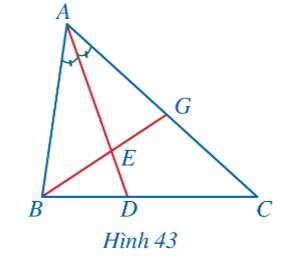
Cho hình thoi ABCD (Hình 4). Điểm M thuộc cạnh AB thỏa mãn \(AB = 3AM\). Hai đoạn thẳng AC và DM cắt nhau tại N. Chứng minh \(ND = 3MN\).
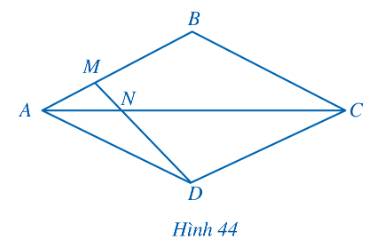
Giải bài toán nêu trong phần mở đầu.
Bài toán: Hình 37 minh họa một phần sân nhà bạn Duy được lát bởi các viên gạch hình vuông khít nhau, trong đó các điểm A, B, C, D là bốn đỉnh của một viên gạch. Bạn Duy đặt một thước gỗ trên mặt sân sao cho thước gỗ luôn đi qua điểm C và cắt tia AB tại M, cắt tia AD tại N. Bạn Duy nhận thấy ta luôn có tỉ lệ thức \(\frac{CM}{CN} = \frac{AM}{AN}\)