Cho tam giác ABC có \(AB = 3,{\rm{ }}BC = 6,{\rm{ }}CA = 5\). Cho O, I là hai điểm phân biệt.
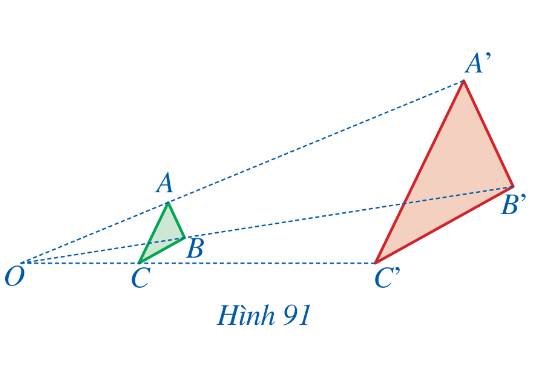
a) Giả sử tam giác A'B'C' là hình đồng dạng phối cảnh của tam giác ABC với điểm O là tâm đồng dạng phối cảnh, tỉ số \(\frac{{A'B'}}{{AB}} = 3\). Hãy tìm độ dài các cạnh của tam giác A'B'C'.
b) Giả sử tam giác A''B''C'' là hình đồng dạng phối cảnh của tam giác ABC với điểm I là tâm đồng dạng phối cảnh, tỉ số \(\frac{{A'B'}}{{AB}} = 3\). Hãy tìm độ dài các cạnh của tam giác A''B''C''.
c) Chứng minh \(\Delta A'B'C' = \Delta A''B''C''\)
Chú ý: Hai tam giác cùng là hình đồng dạng phối cảnh tỉ số k (tâm đồng dạng phối cảnh có thể khác nhau) của một tam giác luôn bằng nhau
a) Vì tam giác A'B'C' là hình đồng dạng phối cảnh của tam giác ABC nên \(\Delta A'B'C' \backsim \Delta ABC\).
\(\begin{array}{l} \Rightarrow \frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}} = \frac{{C'A'}}{{CA}} = 3\\ \Rightarrow \frac{{A'B'}}{3} = \frac{{B'C'}}{6} = \frac{{C'A'}}{5} = 3\\ \Rightarrow A'B' = 9,\,\,B'C' = 18,\,\,C'A' = 15\end{array}\)
b) Vì tam giác A”B”C” là hình đồng dạng phối cảnh của tam giác ABC nên \(\Delta A''B''C'' \backsim \Delta ABC\).
\(\begin{array}{l} \Rightarrow \frac{{A''B''}}{{AB}} = \frac{{B''C''}}{{BC}} = \frac{{C''A''}}{{CA}} = 3\\ \Rightarrow \frac{{A''B''}}{3} = \frac{{B''C''}}{6} = \frac{{C''A''}}{5} = 3\\ \Rightarrow A''B'' = 9,\,\,B''C'' = 18,\,\,C''A'' = 15\end{array}\)
c) Ta có:
\(\begin{array}{l}A'B' = A''B'' = 9\\B'C' = B''C'' = 18\\C'A' = C''A'' = 15\end{array}\)
\( \Rightarrow \Delta A'B'C' = \Delta A''B''C''\)(c-c-c)