Chương I - Hệ thức lượng trong tam giác vuông
Các câu hỏi tương tự
4, cho tg ABC cân tại A, đường cao ứng vs cạnh bên có độ dài bằng h, góc ở đáy của tg bằng α. CMR: \(S^{_{ABC}}=\dfrac{h^2}{4sin\alpha.cos\alpha}\)
Cho tam giác ABC cân ở A, đường cao tương ứng với cạnh đáy có độ dài 15,6 cm , độ cao tương ứng với cạnh bên 12cm. Tính độ dài cạnh đáy BC
GIÚP DÙM MÌNH NHA MÌNH ĐANG CẦN GẤP ^^
1/Chứng minh:
a)tan^2alpha-sin^2alphacdot tan^2alphasin^2alpha
b) cos^2alpha+tan^2alphacdotcos^2alpha1
2/Cho tam giác ABC có BH là đường cao, biết AB 40cm;AC58cm;BC42cm
a) Chứng minh tam giác ABC vuông
b) Tính tỉ số lượng giác của widehat{A}
C)Vẽ HE⊥AB;HF⊥BC. Tính BH ; BE; BF và S_{EFCA}
Đọc tiếp
GIÚP DÙM MÌNH NHA MÌNH ĐANG CẦN GẤP ^^
1/Chứng minh:
a)\(\tan^2\alpha-\sin^2\alpha\cdot tan^2\alpha=sin^2\alpha\)
b) \(\cos^2\alpha+\tan^2\alpha\cdot\cos^2\alpha=1\)
2/Cho tam giác ABC có BH là đường cao, biết AB = 40cm;AC=58cm;BC=42cm
a) Chứng minh tam giác ABC vuông
b) Tính tỉ số lượng giác của \(\widehat{A}\)
C)Vẽ HE⊥AB;HF⊥BC. Tính BH ; BE; BF và \(S_{EFCA}\)
Cho tam giác ABC vuông tại A, AB AC, góc Calpha 45^o , đường trung tuyến AM, đường cao AH, MA MB MC alpha. Chứng minh các công thức :
a) sin2alpha2sinalpha.cosalpha
b) 1+cos2alpha+2cos^2alpha
c) 1-cos2alpha2sin^2alpha
d) sin^2alpha+cos^2alpha1
Đọc tiếp
Cho tam giác ABC vuông tại A, AB < AC, góc \(C=\alpha< 45^o\) , đường trung tuyến AM, đường cao AH, MA = MB = MC = \(\alpha\). Chứng minh các công thức :
a) \(\sin2\alpha=2\sin\alpha.\cos\alpha\)
b) \(1+\cos2\alpha+2\cos^2\alpha\)
c) \(1-\cos2\alpha=2\sin^2\alpha\)
d) \(\sin^2\alpha+\cos^2\alpha=1\)
1. Cho tam giác ABC vuông tại A, đường cao AH . Biết AH6cm , HC - HB 9cm. Tính các độ dài HB,HC.
2. Cho cos a 0,28. Tính các giá trị lượng giác còn lại của góc a.
3. Tìm sin α, cos α biết:
a) tg α frac{3}{4} b) cotg α frac{5}{12}
4. Cho tan α 4. Tính giá trị biểu thức
a) A frac{sin a+cos a}{sin a-cos a} b) B frac{3sin^2a-3cos^2a}{3sin^2a-5cos^2a}
Đọc tiếp
1. Cho tam giác ABC vuông tại A, đường cao AH . Biết AH=6cm , HC - HB = 9cm. Tính các độ dài HB,HC.
2. Cho cos a = 0,28. Tính các giá trị lượng giác còn lại của góc a.
3. Tìm sin α, cos α biết:
a) tg α = \(\frac{3}{4}\) b) cotg α = \(\frac{5}{12}\)
4. Cho tan α = 4. Tính giá trị biểu thức
a) A= \(\frac{\sin a+\cos a}{\sin a-\cos a}\) b) B= \(\frac{3\sin^2a-3\cos^2a}{3\sin^2a-5\cos^2a}\)
4, cho tg ABC cân tại A, đường cao ứng vs cạnh bên có độ dài bằng h, góc ở đáy của tg bằng α. CMR:SABC= 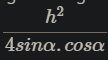
Cho tam giác ABC cân tại A đường cao cạnh bên bằng h góc ở đáy bằng \(\alpha\). CMR:
SABC=\(\frac{h^2}{4sin\alpha.cos\alpha}\)
Chứng minh rằng giá trị của các biểu thức sau không phụ thuộc vào số đo của góc nhọn \(\alpha\)
\(\sin^4\alpha+\sin^2\alpha\cdot\cos^2\alpha+\cos^2\alpha\)
\(\frac{1}{1+\sin\alpha}+\frac{1}{1-\sin\alpha}-2\tan^2\alpha\)
Cho tam giác cân ABC có đáy BC a; ∠BAC 2α ; α 45o, Kẻ các đường cao AE, BF.
a. Tính các cạnh của tam giác BFC theo a và tỉ số lượng giác của góc α.
b. Tính theo a, theo các tỉ số lượng giác của góc α và 2α các cạnh của tam giác ABF, BFC.
c. Từ các kết quả trên, chứng minh các đẳng thức sau:
1) sin2α 2sinαcosα
2) cos2α cos2α - sin2α
3) tg2α frac{2tgalpha}{1-tg^2alpha}
Đọc tiếp
Cho tam giác cân ABC có đáy BC = a; ∠BAC = 2α ; α < 45o, Kẻ các đường cao AE, BF.
a. Tính các cạnh của tam giác BFC theo a và tỉ số lượng giác của góc α.
b. Tính theo a, theo các tỉ số lượng giác của góc α và 2α các cạnh của tam giác ABF, BFC.
c. Từ các kết quả trên, chứng minh các đẳng thức sau:
1) sin2α = 2sinαcosα
2) cos2α = cos2α - sin2α
3) tg2α = \(\frac{2tg\alpha}{1-tg^2\alpha}\)









