Chương I - Hệ thức lượng trong tam giác vuông
Các câu hỏi tương tự
4, cho tg ABC cân tại A, đường cao ứng vs cạnh bên có độ dài bằng h, góc ở đáy của tg bằng α. CMR: \(S^{_{ABC}}=\dfrac{h^2}{4sin\alpha.cos\alpha}\)
4, cho tg ABC cân tại A, đường cao ứng vs cạnh bên có độ dài bằng h, góc ở đáy của tg bằng α. CMR:SABC= 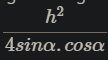
Cho tam giác ABC cân biết góc ở đáy bằng \(\alpha\) và đường cao tương ứng với cạnh bên có độ dài là\(h\) Chứng minh rằng:\(S_{ABC=}\frac{h^2}{4\sin\alpha\cos\alpha}\)
Cho tam giác ABC cân tại A, đường cao ứng với cạnh đáy có độ dài 15,6cm, đường cao ứng với cạnh bên dài 12cm. Tính độ dài cạnh đáy BC. Giải bằng hệ thức lượng trong tam giác vuông. Giúp mình với mình đang cần gấp. Cảm ơn
Cho tam giác ABC cân ở A, đường cao tương ứng với cạnh đáy có độ dài 15,6 cm , độ cao tương ứng với cạnh bên 12cm. Tính độ dài cạnh đáy BC
Bài 1. Cho alpha là góc nhọn. Rút gọn biểu thức: Asin^6alpha+cos^6alpha+3sin^2atimes cos^2alpha
Bài 2. CMR: Nếu 1 Delta có 2 cạnh là a và b, góc nhọn tạo bởi 2 đường thẳng đó là alpha thì diện tích của Delta đó bằng: Sdfrac{1}{2}absinalpha
Bài 3. Cho tanalpha+cosalpha3. Tính giá trị của biểu thức Asinalpha.cosalpha
Đọc tiếp
Bài 1. Cho \(\alpha\) là góc nhọn. Rút gọn biểu thức: \(A=sin^6\alpha+cos^6\alpha+3sin^2a\times cos^2\alpha\)
Bài 2. CMR: Nếu 1 \(\Delta\) có 2 cạnh là a và b, góc nhọn tạo bởi 2 đường thẳng đó là \(\alpha\) thì diện tích của \(\Delta\) đó bằng: \(S=\dfrac{1}{2}absin\alpha\)
Bài 3. Cho \(tan\alpha+cos\alpha=3\). Tính giá trị của biểu thức \(A=sin\alpha.cos\alpha\)
Cho tam giác ABC vuông tại A có đường cao AH, biết AB=3α, AC=4α, với α Là số thực dương.
1)Tính AH theo α
2) tính tan ∠ABC
Cho tam giác ABC cân tại A có cạnh bên =\(\alpha\), đường cao AH có góc HAC=\(\beta\) và đường cao BK. Tính các cạnh của tam giác KBC theo: a, \(\alpha\) và\(\beta\)
b, \(\alpha\) và 2\(\beta\)
giúp mik giải những câu này. cần rất gấp
xét tam giác ABC vuông tại A, AB<AC.góc \(C=\alpha\) <45độ, đường trung tuyến AM, đường cao AH. MA=MB=MC=\(\alpha\). CMR:
a)\(\sin2\alpha=2\sin\alpha.\cos\alpha\)
b)\(1+\cos2\alpha=2\cos^2\alpha\)
c)\(1-\cos2\alpha=2\sin^2\alpha\)









