Question

Cho hình vẽ sau, a//b, A=90 độ, C=130 độ. Tính số đo góc B1 và góc D1.

Answer 1

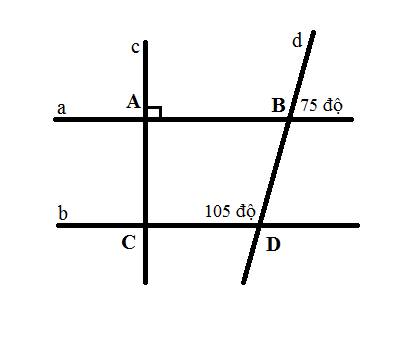
\(\left\{{}\begin{matrix}a//b\\a\perp AB\end{matrix}\right.\Rightarrow b\perp AB\Rightarrow\widehat{B_1}=90^0\\ a//b\Rightarrow\widehat{D_1}+\widehat{C}=180^0\left(2.góc.trong.cùng.phía\right)\\ \Rightarrow\widehat{D_1}=180^0-130^0=50^0\)

Answer 2

Ta có: a//b

Mà \(a\perp AB\)

=> \(b\perp AB\Rightarrow\widehat{B_1}=90^0\)

Ta có: a//b

\(\Rightarrow\widehat{D_1}+\widehat{DCB}=180^0\)(trong cùng phía)

\(\Rightarrow\widehat{D_1}=180^0-\widehat{DCB}=180^0-130^0=50^0\)