Kẻ BK ^CD tại K Þ AB = HK
S A B C D = ( 2 H K ) + 2 K C ) . A H 2 = H C . A H = 96 c m 2
Đúng 1
Bình luận (0)
Violympic toán 8
Các câu hỏi tương tự
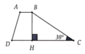
Cho hình thang ABCD (AB//CD) , đường cao AH. Biết AH=6cm , HC=10cm. Tíh diện tích hình bình hành ABCD?
Cho hình thang ABCD, AB//CD, AC vuông góc với BD a, CM: AB^2+CD^2= AD^2+ BC^2 b, AC^2+BD^2=(AB+CD)^2c, Kẻ đường cao AH , , đường trung bình MN của hình thang ABCD biết BD=9cm, AC=12cm. Tính diện tích tứ giác AMHN
Cho hình thang ABCD, AB // CD. Có cạnh AB = 2cm, BC = 8cm, CD = 9cm,\(\widehat{C}\) = 30. Tính diện tích ABCD
Cho hình thang ABCD (AB//CD). Gọi F là giao điểm của hai đường chéo AC và BD.
a, CM: ΔFAB đồng dạng với ΔFCD
b, CM: FA.FD=FB.FC
c, Đường thẳng qua F vuông góc với AB tại M và cắt CD tại N, biết FB=3cm; FD= 6cm; FM= 2cm; CD= 8cm. Hãy tính diện tích ΔFCD
2.Cho hình thang ABCD (AB//CD). Gọi F là giao điểm của hai đường chéo AC và BD.a, CM: ΔFAB đồng dạng với ΔFCDb, CM: FA.FDFB.FCc, Đường thẳng qua F vuông góc với AB tại M và cắt CD tại N, biết FB3cm; FD 6cm; FM 2cm; CD 8cm. Hãy tính diện tích ΔFCD3.Cho tam giác ABC vuông tại A có AB 12cm, AC 16cm. kẻ đường cao AH.a) Cm tam giác HBA đồng dạng tam giác ABC.b) Tính BC,AH,BHc) gọi AD là phân giac góc BAC ( D thuộc BC)tính diện tích tam giac AHD (làm tròn đến chữ số thâp phân thứ nhất)
Đọc tiếp
2.
Cho hình thang ABCD (AB//CD). Gọi F là giao điểm của hai đường chéo AC và BD.
a, CM: ΔFAB đồng dạng với ΔFCD
b, CM: FA.FD=FB.FC
c, Đường thẳng qua F vuông góc với AB tại M và cắt CD tại N, biết FB=3cm; FD= 6cm; FM= 2cm; CD= 8cm. Hãy tính diện tích ΔFCD
3.
Cho tam giác ABC vuông tại A có AB = 12cm, AC =16cm. kẻ đường cao AH.
a) Cm tam giác HBA đồng dạng tam giác ABC.
b) Tính BC,AH,BH
c) gọi AD là phân giac góc BAC ( D thuộc BC)
tính diện tích tam giac AHD (làm tròn đến chữ số thâp phân thứ nhất)
Cho hình thang ABCD (AB//CD). Gọi F là giao điểm của hai đường chéo AC và BD.
a, CM: ΔFAB đồng dạng với ΔFCD
b, CM: FA.FD=FB.FC
c, Đường thẳng qua F vuông góc với AB tại M và cắt CD tại N, biết FB=3cm; FD= 6cm; FM= 2cm; CD= 8cm. Hãy tính diện tích ΔFCD
Cho hình thang ABCD cân có AB // CD, AB < CD, AH & BK là các đường cao . CM : HB = KC & DH = \(\dfrac{CD-AB}{2}\)
Cho hình thang cân ABCD có AB // CD, AB bé hơn CD.Kẻ 2 đường cao AH và BK [H và K thuộc CD], AB = 6 cm , CD = 15cm . Tính HD và KC.
Cho hình thang cân ABCD(AB//CD), DC là đáy lớn, AH là đường cao(H thuộc DC) và HC = 5cm. Tính độ dài đường trung bình của hình thang ABCD