Bài 5: Tiên để Ơ - clit về đường thẳng song song
Các câu hỏi tương tự
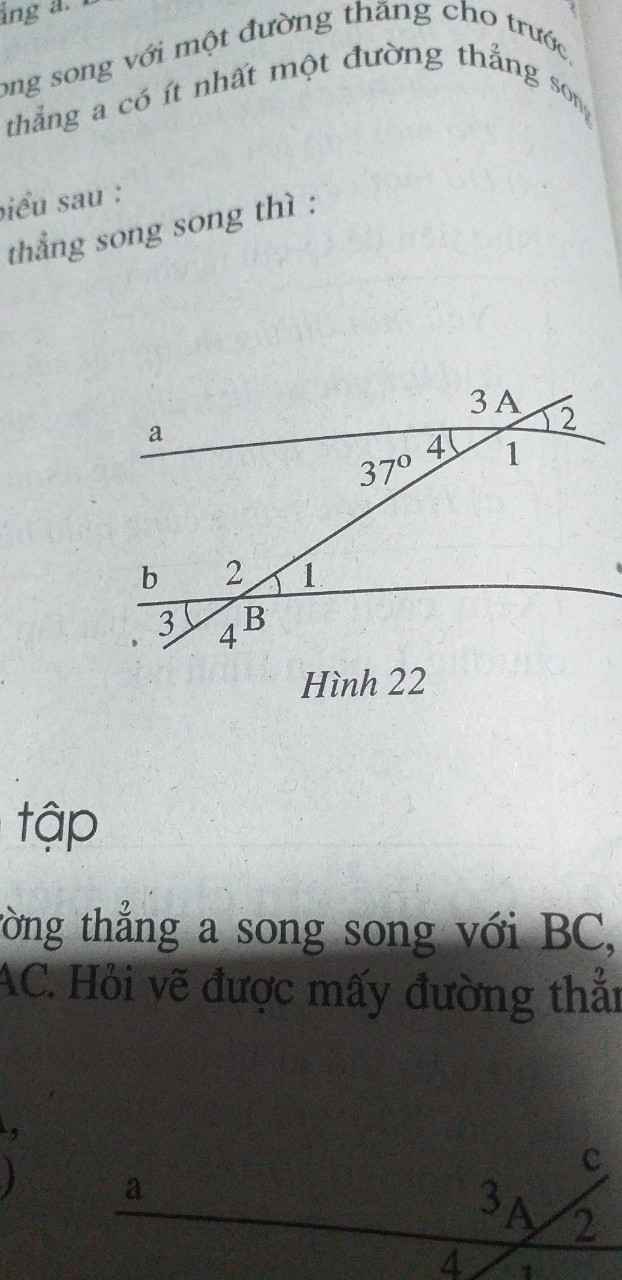
Hình 22 cho biết a // b và \(\widehat{A}_4\) = \(37^o\) .
a) Tính \(\widehat{B_1}\) .
b) So sánh \(\widehat{A_1}\) và \(\widehat{B_4}\) .
c) Tính \(\widehat{B_2}\)
Hình 22 cho biết a // b và \(\widehat{A}_4=37^0\)
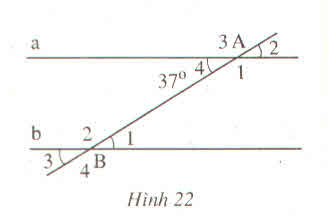
a) Tính \(\widehat{B_1}\)
b) So sánh \(\widehat{A_1}\) và \(\widehat{B_4}\)
c) Tính \(\widehat{B_2}\)
Hình 23 cho biết a // b và c cắt a tại A, cặt b tại B. Hãy điền vào chỗ trống (...) trong các câu sau :
a) widehat{A}_1..... (vì là cặp góc so le trong)
b) widehat{A}_2....... (vì là cặp góc đồng vị)
c) widehat{B_3+}widehat{A}_4.......(vì........)
d) widehat{A}_2widehat{B_4} (vì ...........)
Đọc tiếp
Hình 23 cho biết a // b và c cắt a tại A, cặt b tại B. Hãy điền vào chỗ trống (...) trong các câu sau :
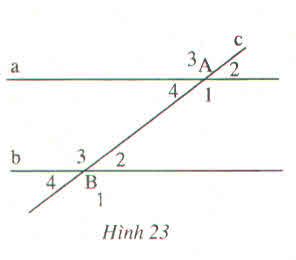
a) \(\widehat{A}_1=.....\) (vì là cặp góc so le trong)
b) \(\widehat{A}_2=.......\) (vì là cặp góc đồng vị)
c) \(\widehat{B_3+}\widehat{A}_4=.......\)(vì........)
d) \(\widehat{A}_2=\widehat{B_4}\) (vì ...........)
Cho Delta ABC , trên nửa mặt phẳng bờ là đường thẳng AC không chứa B , vẽ tia AD sao cho widehat{DAC}widehat{ACB} . Trên nửa mặt phẳng bờ là đường thẳng AB không chứa C , vẽ tia AE sao cho widehat{EAB}widehat{ABC} . Chứng minh ba điểm E , A , D thẳng hàng . ( Biết Delta ABCwidehat{A}+widehat{B}+widehat{C}180^o)
Đọc tiếp
\(Cho\) \(\Delta ABC\) , trên nửa mặt phẳng bờ là đường thẳng AC không chứa B , vẽ tia \(AD\) sao cho \(\widehat{DAC}=\widehat{ACB}\) . Trên nửa mặt phẳng bờ là đường thẳng \(AB\) không chứa C , vẽ tia \(AE\) sao cho \(\widehat{EAB}=\widehat{ABC}\) . Chứng minh ba điểm E , A , D thẳng hàng . ( Biết \(\Delta ABC=\widehat{A}+\widehat{B}+\widehat{C}=180^o\))
Cho \(\widehat{xoy}\) và \(\widehat{x'o'y'}\) đều nhọn mà Ox// O'x', Oy//O'y'
Chứng minh \(\widehat{xoy}=x'o'y'\). Gợi ý : gọi giao của Oy và O'x' là A
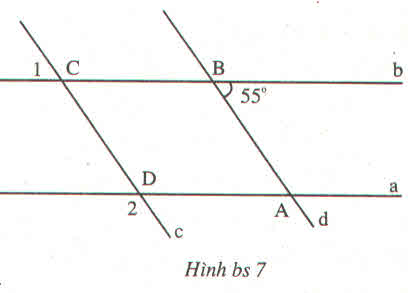
Cho hình bs 7 (đường thẳng a song song với đường thẳng b và đường thẳng c song song với đường thẳng d)
Cho biết số đo của các góc \(\widehat{C}_1,\widehat{D}_2\) và giải thích cách tìm ra kết quả ?
Trên hình 7, hai đường thẳng a, b song song với nhau, đường thẳng c cắt a tại A và cắt b tại B
a) Lấy một cặp góc so le trong (chẳng hạn cặp A_4,B_1) rồi đo xem hai góc đó có bằng nhau hay không
b) Hãy lí luận vì sao widehat{A}_4widehat{B}_1 theo gợi ý sau :
- Nếu widehat{A}_4newidehat{B}_1 thì qua A ta vẽ tia AP sao cho widehat{PAB}widehat{B}_1
- Thế thì AP // b, vì sao ?
- Qua A, vừa có a // b, vừa có AP // b, thì sao ?
- Kết luận : Đường thẳng AP và đường thẳng a chỉ là một. Nói cách...
Đọc tiếp
Trên hình 7, hai đường thẳng a, b song song với nhau, đường thẳng c cắt a tại A và cắt b tại B
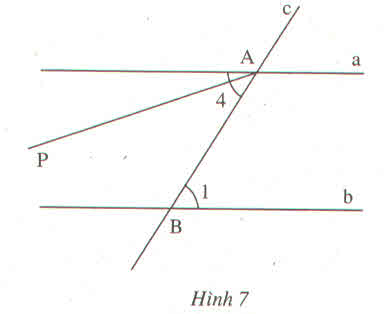
a) Lấy một cặp góc so le trong (chẳng hạn cặp \(A_4,B_1\)) rồi đo xem hai góc đó có bằng nhau hay không
b) Hãy lí luận vì sao \(\widehat{A}_4=\widehat{B}_1\) theo gợi ý sau :
- Nếu \(\widehat{A}_4\ne\widehat{B}_1\) thì qua A ta vẽ tia AP sao cho \(\widehat{PAB}=\widehat{B}_1\)
- Thế thì AP // b, vì sao ?
- Qua A, vừa có a // b, vừa có AP // b, thì sao ?
- Kết luận : Đường thẳng AP và đường thẳng a chỉ là một. Nói cách khác \(\widehat{PAB}=\widehat{A}_4\), từ đó \(\widehat{A}_4=\widehat{B}_1\)
Cho hình bs 7 (đường thẳng a song song với đường thẳng b và đường thẳng c song song với đường thẳng d)
Cho biết số đo của các góc \(\widehat{C1}\) , \(\widehat{D2}\) và giải thích cách tìm ra kết quả ?

1. Cho a vuông góc b tại A, c vuông góc b tại C
Chứng tỏ a // c
2. Cho a//b, c vuông góc b tại M
chứng tỏ a vuông góc c
3. Cho d//a, d//b
Chứng tỏ a//b
4. Cho đoạn thẳng AB, trên cùng 1 nửa mặt phẳng có bờ là đường thẳng AB vẽ tia Ax, By trong đó widehat{BAx}infty , widehat{ABy}4infty. Tính widehat{BAx} để Ax//By
Đọc tiếp
1. Cho a vuông góc b tại A, c vuông góc b tại C
Chứng tỏ a // c
2. Cho a//b, c vuông góc b tại M
chứng tỏ a vuông góc c
3. Cho d//a, d//b
Chứng tỏ a//b
4. Cho đoạn thẳng AB, trên cùng 1 nửa mặt phẳng có bờ là đường thẳng AB vẽ tia Ax, By trong đó \(\widehat{BAx}=\infty\) , \(\widehat{ABy}=4\infty\). Tính \(\widehat{BAx}\) để Ax//By











