Bài 7: Định lí
Nội dung lý thuyết
1. Định lí
- Tính chất "Hai góc đối đỉnh thì bằng nhau" được khẳng định là đúng không phải bằng đo trực tiếp mà bằng suy luận. Một tính chất như thế được gọi là một định lí.
Ta có thể hiểu rằng:
Định lí là một khẳng định suy ra từ những khẳng định được coi là đúng.
Ví dụ: Ta đã biết tính chất "Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng kia". Đây cũng là một định lí.
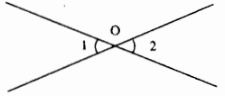
*Trong định lí "Hai góc đối đỉnh thì bằng nhau" (hình vẽ dưới đây), điều đã cho "\(\widehat{O_1}\) và \(\widehat{O_2}\) là hai góc đối đỉnh" là phần giả thiết của định lí, điều phải suy ra "\(\widehat{O_1}=\widehat{O_2}\)" là kết luận của định lí.
Ta có thể hiểu rằng
Giả thiết của định lí là điều đã cho.
Kết luận của định lí là điều phải suy ra.
Ví dụ : Trong định lí "Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng kia" (hình vẽ sau)

Giả thiết của định lí là: đường thẳng \(a\) song song với đường thẳng \(b\) , đường thẳng \(c\) vuông góc với đường thẳng \(a\)
Kết luận của định lí là: đường thẳng \(c\) vuông góc với đường thẳng \(b\)
Chú ý: - Khi định lí được phát biểu dưới dạng "Nếu...thì...", phần nằm giữa từ "Nếu" và từ "thì" là phần giả thiết, phần nằm sau từ "thì" là phần kết luận.
- Giả thiết và kết luận của định lí được kí hiệu lần lượt là GT và KL.
@1312515@
2. Chứng minh định lí
Chứng minh định lí là dùng lập luận để từ giả thiết suy ra kết luận.
Ví dụ: Chứng minh định lí sau: "Góc tạo bởi hai tia phân giác của hai góc kề bù là một góc vuông"
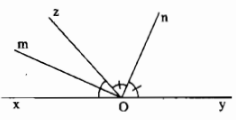
| GT | \(\widehat{xOz}\) và \(\widehat{zOy}\) kề bù \(Om\) là tia phân giác của góc \(\widehat{xOz}\) \(On\) là tia phân giác của góc \(\widehat{zOy}\) |
| KL | \(\widehat{mOn}=90^0\) |
Chứng minh:
\(Om\) là tia phân giác của \(\widehat{xOz}\) \(\Rightarrow\) \(\widehat{mOz}=\dfrac{1}{2}\widehat{xOz}\) (1)
\(On\) là tua phân giác của \(\widehat{zOy}\) \(\Rightarrow\) \(\widehat{zOn}=\dfrac{1}{2}\widehat{zOy}\) (2)
Từ (1) và (2) \(\Rightarrow\) \(\widehat{mOz}+\widehat{zOn}=\dfrac{1}{2}\left(\widehat{xOz}+\widehat{zOy}\right)\)
Vì tia \(Oz\) nằm giữa tia \(Om\) và tia \(On\) và \(\widehat{xOz}\) và \(\widehat{zOy}\) là hai góc kề bù
\(\Rightarrow\) \(\widehat{mOn}=\dfrac{1}{2}.180^0=90^0\)
\(\Rightarrow\) ĐPCM
@54423@