Chương III - Góc với đường tròn
Các câu hỏi tương tự
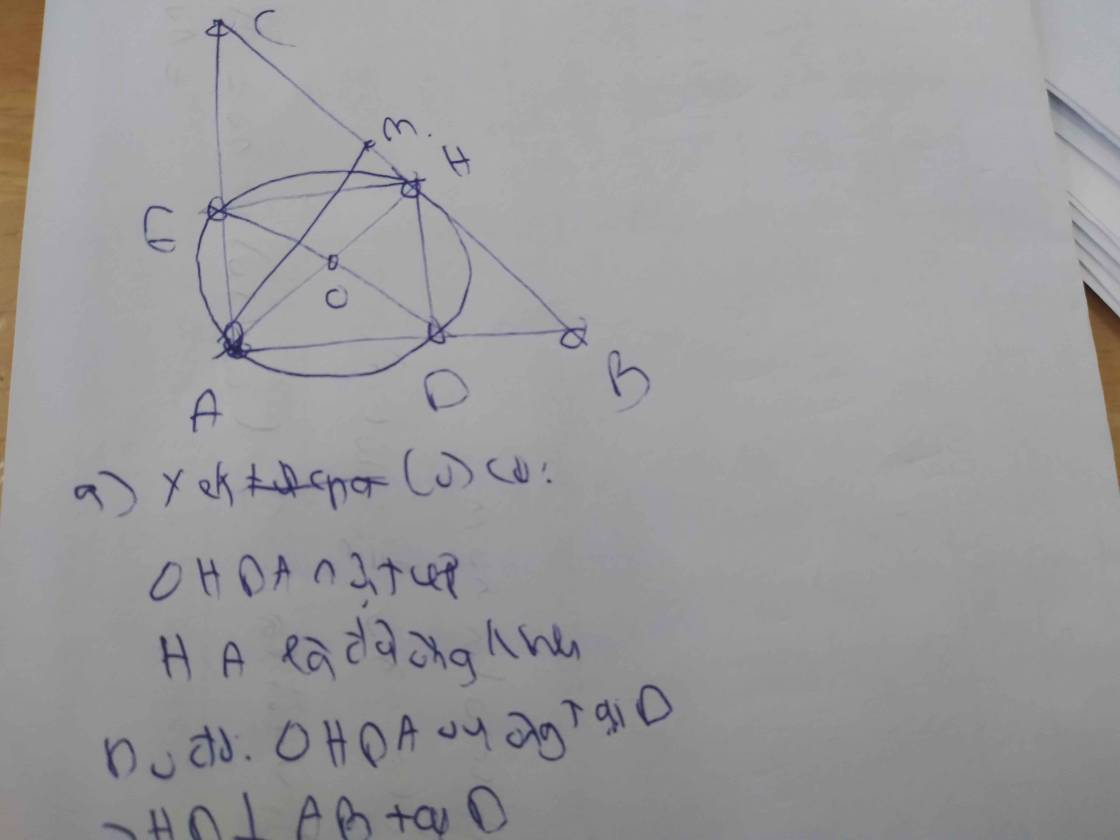
Cho tam giác ABC có 3 góc nhọn (ABBC,AC) nội tiếp (O). Kẻ các đường cao BD,CE cắt nhau tại H (D thuộc AC, E thuộc AB)a, Chứng minh BCDE là tứ giác nội tiếpb, Chứng minh DA.DC DH.DBc, Vẽ đường tròn tâm H, bán kính HA cắt các tia AB, AC lần lượt tại M,N. Chứng minh OA vuông góc với MN.d, Các tiếp tuyến tại M,N của (H,HA) cắt nhau tại P. Chứng minh AP đi qua trung điểm của BC.
Đọc tiếp
Cho tam giác ABC có 3 góc nhọn (AB<BC,AC) nội tiếp (O). Kẻ các đường cao BD,CE cắt nhau tại H (D thuộc AC, E thuộc AB)
a, Chứng minh BCDE là tứ giác nội tiếp
b, Chứng minh DA.DC= DH.DB
c, Vẽ đường tròn tâm H, bán kính HA cắt các tia AB, AC lần lượt tại M,N. Chứng minh OA vuông góc với MN.
d, Các tiếp tuyến tại M,N của (H,HA) cắt nhau tại P. Chứng minh AP đi qua trung điểm của BC.
cho tam giác ABC vuông tại A đường cao AH. Đường tròn tâm E đường kính BH cắt AB tại M( M khác B), đường trong tâm F đường kính HC cắt AC tại N(N khác C)a)Chứng minh AM.ABAN.AC và AN.ACMN2b)Gọi I là trung điểm của EF, O là giao điểm của AH và MN. Chứng minh IO vuông góc với đường thẳng MNc)Chứng minh 4(EN2+FM2)BC2+6AH2
Đọc tiếp
cho tam giác ABC vuông tại A đường cao AH. Đường tròn tâm E đường kính BH cắt AB tại M( M khác B), đường trong tâm F đường kính HC cắt AC tại N(N khác C)
a)Chứng minh AM.AB=AN.AC và AN.AC=MN2
b)Gọi I là trung điểm của EF, O là giao điểm của AH và MN. Chứng minh IO vuông góc với đường thẳng MN
c)Chứng minh 4(EN2+FM2)=BC2+6AH2
Cho tam giác ABC cân tại A nội tiếp đường tròn (O). Từ một điểm M tùy ý trên dây BC, kẻ các đường thẳng song song với AC và AB, chúng cắt AB và AC lần lượt tại P và Q. Gọi D là điểm đối xứng của M qua đường thẳng PQ.
Chứng minh: D nằm trên đường tròn (O).
Cho tam giác ABC nội tiếp (O) đường kính BC có AB AC , hai tiếp tuyến tại A và B cắt nhau tại M .1) Chứng minh: Tứ giác MAOB nội tiếp đường tròn và xác định tâm I của đường tròn này.2) Chứng minh : .3) Đường cao AH của tam giác ABC cắt CM tại N. Chứng minh: N là trung điểm của AH.
Đọc tiếp
Cho tam giác ABC nội tiếp (O) đường kính BC có AB > AC , hai tiếp tuyến tại A và B cắt nhau tại M .
1) Chứng minh: Tứ giác MAOB nội tiếp đường tròn và xác định tâm I của đường tròn này.
2) Chứng minh : ![]() .
.
3) Đường cao AH của tam giác ABC cắt CM tại N. Chứng minh: N là trung điểm của AH.
Cho tam giác ABC nhọn. Vẽ đường cao BD và CE của tam giác, biết D thuộc cạnh AC, E thuộc cạnh AB. CE và BD cắt nhau tại H. Gọi I, K lần lượt là trung điểm của BC và AH. Chứng minh rằng: a) Bốn điểm B, C, E, D cùng thuộc đường tròn tâm I. I. b) Tứ giác IEKD nội tiếp được trong một đường tròn.
Cho tam giác ABC nội tiếp đường tròn tâm O, gọi E,D lần lượt là giao điểm của các tia phân giác trong và ngoài của 2 góc B và C. Đường thẳng ED cắt BC tại I, cắt cung nhỏ BC ở M chứng minh
a) ba điểm AED thẳng hàng
b) chứng minh tứ giác BECD nội tiếp
c) Tìm 2 cặp tam giác đồng dạng
Help!! mời các cao nhân vào giúp
Cho tam giác nhọn ABC nội tiếp đường tròn (O) . Các đường cao BD, CE ( D thuộc AC, E thuộc AB ) cắt nhau tại H . Đường thẳng DE cắt đường thẳng BC tại G .1) Chứng minh tứ giác BCDE là tứ giác nội tiếp được trong đường tròn .2) Chứng minh : GB . GC GE . GD .3) Đường thẳng AG cắt đường tròn (O) tại điểm M . Chứng minh : góc MAB góc MDG .Mình cần câu 3 thôi ạ (k cần giải chi tiết, chỉ cần nêu ý)
Đọc tiếp
Cho tam giác nhọn ABC nội tiếp đường tròn (O) . Các đường cao BD, CE ( D thuộc AC, E thuộc AB ) cắt nhau tại H . Đường thẳng DE cắt đường thẳng BC tại G .
1) Chứng minh tứ giác BCDE là tứ giác nội tiếp được trong đường tròn .
2) Chứng minh : GB . GC = GE . GD .
3) Đường thẳng AG cắt đường tròn (O) tại điểm M . Chứng minh : góc MAB = góc MDG .
Mình cần câu 3 thôi ạ (k cần giải chi tiết, chỉ cần nêu ý)
Cho tam giác ABC nhọn nội tiếp đường tròn (O;R). Gọi Q là trung điểm của BC và các đường cao AD, BE, CF cắt nhau tại H.
a) Chứng minh : AH = 2OQ
b) Chứng minh rằng nếu : AB + AC = 2BC thì sinB + sin C = 2sin A
c) Cho BC = \(R\sqrt{2}\), chứng minh : AE * FH + AF * HE = \(R^2\sqrt{2}\)
Cho đường tròn đường kính BC cố định. Trên tia đối của BC lấy điểm A (khác B). Kẻ tiếp tuyến AM với đường tròn tâm (O), M là tiếp điểm. Qua A kẻ đường thẳng d vuông góc với AC, tia CM cắt d tại D.
a) Chứng minh tứ ADMB là tứ giác nội tiếp
b) Kẻ tia Mx sao cho MB là phân giác của góc AMx. Chứng minh AB.AC=AH.AO