\(\frac{1}{x}+\frac{1}{y}\ge\frac{4}{x+y}\)
\(\Leftrightarrow\frac{x+y}{xy}\ge\frac{4}{x+y}\)
\(\Leftrightarrow\left(x+y\right)^2\ge4xy\)
\(\Leftrightarrow\left(x-y\right)^2\ge0\) (luôn đúng)
Vậy BĐT đã cho đúng. Dấu "=" xảy ra khi \(x=y\)
\(\frac{1}{x}+\frac{1}{y}\ge\frac{4}{x+y}\)
\(\Leftrightarrow\frac{x+y}{xy}\ge\frac{4}{x+y}\)
\(\Leftrightarrow\left(x+y\right)^2\ge4xy\)
\(\Leftrightarrow\left(x-y\right)^2\ge0\) (luôn đúng)
Vậy BĐT đã cho đúng. Dấu "=" xảy ra khi \(x=y\)
Cho 3 số thực dương x, y, z. Chứng minh rằng
\(\frac{1}{x^3+y^3+xyz}+\frac{1}{y^3+z^3+xyz}+\frac{1}{x^3+z^3+xyz}\le\frac{1}{xyz}\)
Bài 1: Cho a,b dương sao cho a+b=1. Chứng minh rằng: \(\frac{a^2}{a+2b}+\frac{b^2}{a+2b}\ge\frac{1}{3}\)
bài 2: Cho x,y là các số thực dương thỏa mãn x+y=2019. tìm giá trị nhỏ nhất của biểu thức P= \(\frac{x}{\sqrt{2019-x}}+\frac{y}{\sqrt{2019-y}}\)
bài 3: Cho x>0, y>0 là những số thay đổi thỏa mãn \(\frac{2018}{x}+\frac{2019}{y}=1\). tìm giá trị nhỏ nhất của biểu thức P= x+y
Mọi người giúp mình câu này với ạ. Mình đang cần gấp ạ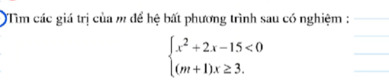
\(\frac{1}{x^3\left(y+z\right)}+\frac{1}{y^3\left(x+z\right)}+\frac{1}{z^3\left(x+y\right)}\ge\frac{3}{2}\) với abc=1
Câu 4. Cho a,b,c là ba số thực dương . Chứng minh rằng \(\frac{a^2}{b}+\frac{b^2}{c}+\frac{c^2}{a}\ge a+b+c\).
Tìm GTNN của hàm số y = \(\frac{4}{x}+\frac{1}{1-x}\) với 0 < x < 1.
Câu 4. Cho a,b,c là ba số thực dương . Chứng minh rằng \(\frac{ab}{c}+\frac{bc}{a}+\frac{ca}{b}\ge a+b+c\)
B7 Tìm giá trị nhỏ nhất của hàm số y=\(\frac{3}{-x^2+4x-8}\)
B8 Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số a y=\(\frac{3-4x}{x^2+1}\)
b y=\(\frac{4x^2+6x+10}{x^2+2x+3}\)
c y=\(\frac{x+1}{x^2+x+1}\)
Cho x,y là hai số thực thỏa mãn x > y
và xy = 1000. Biết biểu thức \(F=\frac{x^2+y^2}{x-y}\)
đạt giá trị nhỏ nhất khi \(\hept{\begin{cases}x=a\\y=b\end{cases}}\)
Tinh \(P=\frac{a^2+b^2}{1000}\)