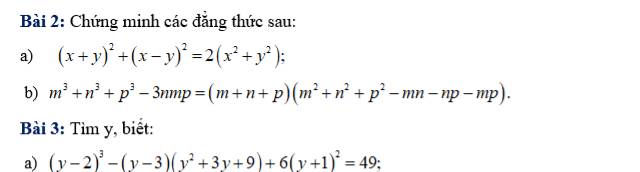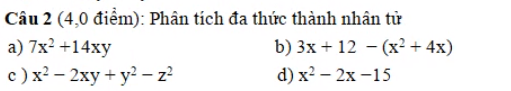Bài 3:
a: \(\left(y-2\right)^3-\left(y-3\right)\left(y^2+3y+9\right)+6\left(y+1\right)^2=49\)
=>\(y^3-6y^2+12y-8-\left(y^3-27\right)+6\left(y^2+2y+1\right)=49\)
=>\(y^3-6y^2+12y-8-y^3+27+6y^2+12y+6=49\)
=>\(24y+25=49\)
=>24y=24
=>y=1
Bài 2:
a: \(\left(x+y\right)^2+\left(x-y\right)^2\)
\(=x^2+2xy+y^2+x^2-2xy+y^2\)
\(=2x^2+2y^2=2\left(x^2+y^2\right)\)
b: \(m^3+n^3+p^3-3mnp\)
\(=\left(m+n\right)^3-3mn\left(m+n\right)+p^3-3mnp\)
\(=\left(m+n\right)^3+p^3-3mn\left(m+n\right)-3mpn\)
\(=\left(m+n+p\right)\left[\left(m+n\right)^2-p\left(m+n\right)+p^2\right]-3mn\left(m+n+p\right)\)
\(=\left(m+n+p\right)\left(m^2+2mn+n^2-pm-pn+p^2-3mn\right)\)
\(=\left(m+n+p\right)\left(m^2+n^2+p^2-mn-mp-np\right)\)
Bài 2
a) \(VT=\left(x+y\right)^2+\left(x-y\right)^2\)
\(=x^2+2xy+y^2+x^2-2xy+y^2\)
\(=\left(x^2+x^2\right)+\left(2xy-2xy\right)+\left(y^2+y^2\right)\)
\(=2x^2+2y^2\)
\(=2\left(x^2+y^2\right)\)
\(=VP\)
Vậy \(\left(x+y\right)^2+\left(x-y^2\right)=2\left(x^2+y^2\right)\)
b) \(VP=\left(m+n+p\right)\left(m^2+n^2+p^2-mn-np-mp\right)\)
\(=m^3+mn^2+mp^2-m^2n-mnp-m^2p+m^2n+n^3+np^2-mn^2-n^2p-mnp+m^2p+n^2p+p^3-mnp-np^2-mp^2\)
\(=m^3+n^3+p^3+\left(mn^2-mn^2\right)+\left(mp^2-mp^2\right)+\left(-m^2n+m^2n\right)+\left(-mnp-mnp-mnp\right)+\left(n^2p-n^2p\right)+\left(np^2-np^2\right)+\left(m^2p-m^2p\right)\)
\(=m^3+n^3+p^3-3mnp\)
\(=VP\)
Vậy \(m^3+n^3+p^3-3mnp=\left(m+n+p\right)\left(m^2+n^2+p^2-mn-np-mp\right)\)
Bài 3
a) \(\left(y-2\right)^3-\left(y-3\right)\left(y^2+3y+9\right)+6\left(y+1\right)^2=49\)
\(y^3-6y^2+12y-8-y^3+27+6y^2+12y+6=49\)
\(\left(y^3-y^3\right)+\left(-6y^2+6y^2\right)+\left(12y+12y\right)+25=49\)
\(24y=49-25\)
\(24y=24\)
\(y=\dfrac{24}{24}\)
\(y=1\)