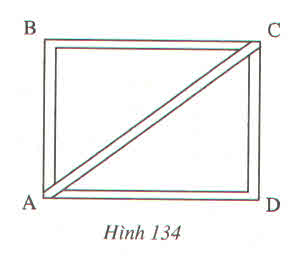
độ dài đường chéo AC là
\(\sqrt{48^2+36^2}=\sqrt{2304+1296}=\sqrt{3600}=60\)(cm)
vậy độ dài đường chéo AC là 60cm
Giải:
Theo định lí Pytago, ta có:
AC2= AD2 +CD2
= 482 + 362
= 2304 + 1296= 3600
AC= 60 (cm)
Vì khung ABCD là khung chữ nhật=>Góc ADC vuông
Theo định lí Pi-ta-go có:
\(AD^2\)+\(CD^2\)=\(AC^2\)
\(48^2\)+\(36^2\)=\(AC^2\)
3600=\(AC^2\)
AC=\(\sqrt{3600}\)=60
![]()
Theo định lí Pytago, ta có:
AC2= AD2 +CD2
= 482 + 362
= 2304 + 1296= 3600
AC= 60 (cm)
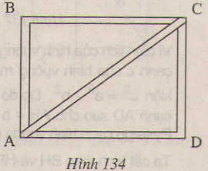
Theo định lí Pytago, ta có:
AC2= AD2 +CD2
= 482 + 362
= 2304 + 1296= 3600
AC= 60 (cm)
Vì tam giác ADC vuông tại D nên:
Áp dụng định lý PI-TA-GO vào tam giác ADC:
\(AC^2=AD^2+DC^2\)
\(AC^2=48^2+36^2\)
\(AC^2=3600\)
AC= 0
Vậy...