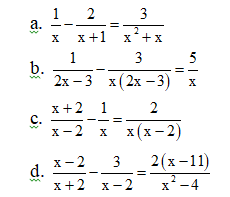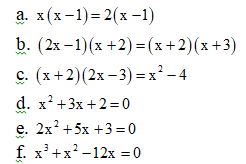Question

Bài 1:

Bài 2:

Answer 1

Tách nhỏ câu hỏi ra bạn

Answer 2

Bài 1 : 

a, đk x khác -1 ; 0 

\(x+1-2x=3\Leftrightarrow x=-2\)(tm) 

b, đk : x khác 0 ; 3/2 

\(x-3=10x-15\Leftrightarrow9x=12\Leftrightarrow x=\dfrac{4}{3}\)(tm) 

c, đk x khác 0 ; 2 

\(x^2+2x-x+2=2\Leftrightarrow x\left(x+1\right)=0\Leftrightarrow x=0\left(ktm\right);x=-1\)

d, đk : x khác -2 ; 2 

\(x^2-4x+4-3x-6=2x-22\Leftrightarrow x^2-9x+20=0\)

\(\Leftrightarrow\left(x-4\right)\left(x-5\right)=0\Leftrightarrow x=4;x=5\)

 

 

Answer 3

Bài 1:

a) \(\dfrac{1}{x}-\dfrac{2}{x+1}=\dfrac{3}{x^2+x}\) (1)

ĐKXĐ: \(x\ne0;x\ne-1\)

\(\left(1\right)\Leftrightarrow\dfrac{x+1}{x\left(x+1\right)}-\dfrac{2x}{x\left(x+1\right)}=\dfrac{3}{x\left(x+1\right)}\)

\(\Leftrightarrow x+1-2x=3\)

\(\Leftrightarrow-x=2\)

\(\Leftrightarrow x=-2\) (nhận)

Vậy S = {\(-2\)}

Answer 4

Bài 1:

b) \(\dfrac{1}{2x-3}-\dfrac{3}{x\left(2x-3\right)}=\dfrac{5}{x}\) (2)

ĐKXĐ: \(x\ne0;x\ne\dfrac{3}{2}\)

\(\left(2\right)\Leftrightarrow\dfrac{x}{x\left(2x-3\right)}-\dfrac{3}{x\left(2x-3\right)}=\dfrac{5\left(2x-3\right)}{x\left(2x-3\right)}\)

\(\Leftrightarrow x-3=5\left(2x-3\right)\)

\(\Leftrightarrow x-3=10x-15\)

\(\Leftrightarrow-9x=-12\)

\(\Leftrightarrow x=\dfrac{4}{3}\) (nhận)

Vậy S = \(\left\{\dfrac{4}{3}\right\}\)

Answer 5

Bài 2 : 

a, \(x\left(x-1\right)-2\left(x-1\right)=0\Leftrightarrow\left(x-2\right)\left(x-1\right)=0\Leftrightarrow x=1;x=2\)

b, \(\left(2x-1\right)\left(x+2\right)-\left(x+2\right)\left(x+3\right)=0\)

\(\Leftrightarrow\left(x+2\right)\left(x-4\right)=0\Leftrightarrow x=-2;x=4\)

c, \(\left(x+2\right)\left(2x-3\right)-\left(x-2\right)\left(x+2\right)=0\Leftrightarrow\left(x+2\right)\left(x-1\right)=0\Leftrightarrow x=-2;x=1\)

d, \(x^2+2x+x+2=0\Leftrightarrow x\left(x+2\right)+x+2=0\Leftrightarrow\left(x+1\right)\left(x+2\right)=0\Leftrightarrow x=-2;x=-1\)

e, \(2x^2+2x+3x+3=0\Leftrightarrow2x\left(x+1\right)+3\left(x+1\right)=0\Leftrightarrow\left(2x+3\right)\left(x+1\right)=0\Leftrightarrow x=-\dfrac{3}{2};x=-1\)

f, \(x\left(x^2+x-12\right)=0\Leftrightarrow x\left(x+4\right)\left(x-3\right)=0\Leftrightarrow x=0;x=3;x=-4\)

Answer 6

Bài 1:

c) \(\dfrac{x+2}{x-2}-\dfrac{1}{x}=\dfrac{2}{x\left(x-2\right)}\) (3)

ĐKXĐ: \(x\ne0;x\ne2\)

\(\left(3\right)\Leftrightarrow\dfrac{x\left(x+2\right)}{x\left(x-2\right)}-\dfrac{x-2}{x\left(x-2\right)}=\dfrac{2}{x\left(x-2\right)}\)

\(\Leftrightarrow x\left(x+2\right)-\left(x-2\right)=2\)

\(\Leftrightarrow x^2+2x-x+2-2=0\)

\(\Leftrightarrow x^2+x=0\)

\(\Leftrightarrow x\left(x+1\right)=0\)

\(\Leftrightarrow x=0\) (loại) hoặc \(x+1=0\)

\(x+1=0\)

\(\Leftrightarrow x=-1\) (nhận)

Vậy \(S=\left\{-1\right\}\)

Answer 7

Bài 1:

d) \(\dfrac{x-2}{x+2}-\dfrac{3}{x-2}=\dfrac{2\left(x-11\right)}{x^2-4}\) (4)

ĐKXĐ: \(x\ne2;x\ne-2\)

\(\left(4\right)\Leftrightarrow\dfrac{\left(x-2\right)^2}{\left(x+2\right)\left(x-2\right)}-\dfrac{3\left(x+2\right)}{\left(x+2\right)\left(x-2\right)}=\dfrac{2\left(x-11\right)}{\left(x+2\right)\left(x-2\right)}\)

\(\Leftrightarrow\left(x-2\right)^2-3\left(x+2\right)=2\left(x-11\right)\)

\(\Leftrightarrow x^2-4x+4-3x-6=2x-22\)

\(\Leftrightarrow x^2-9x+20=0\)

\(\Leftrightarrow x^2-4x-5x+20=0\)

\(\Leftrightarrow\left(x^2-4x\right)-\left(5x-20\right)=0\)

\(\Leftrightarrow x\left(x-4\right)-5\left(x-4\right)=0\)

\(\Leftrightarrow\left(x-4\right)\left(x-5\right)=0\)

\(\Leftrightarrow x-4=0\) hoặc \(x-5=0\)

*) \(x-4=0\)

\(\Leftrightarrow x=4\) (nhận)

*) \(x-5=0\)

\(\Leftrightarrow x=5\) (nhận)

Vậy \(S=\left\{4;5\right\}\)